
【题目】数据0.7,1,0.8,0.9,1.1的方差是 .
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
【题目】用数学归纳法证明12+22+…+(n﹣1)2+n2+(n﹣1)2+…+22+12═ ![]() 时,由n=k的假设到证明n=k+1时,等式左边应添加的式子是( )
时,由n=k的假设到证明n=k+1时,等式左边应添加的式子是( )
A.(k+1)2+2k2
B.(k+1)2+k2
C.(k+1)2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a,b∈R且a<b,若a3eb=b3ea , 则下列结论中一定正确的个数是( ) ①a+b>6;②ab<9;③a+2b>9;④a<3<b.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式﹣2<|x﹣1|﹣|x+2|<0的解集为M,a、b∈M,
(1)证明:| ![]() a+
a+ ![]() b|<
b|< ![]() ;
;
(2)比较|1﹣4ab|与2|a﹣b|的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的左、右焦点分别为F1 , F2 , 上顶点为B,若△BF1F2的周长为6,且点F1到直线BF2的距离为b. (Ⅰ)求椭圆C的方程;
的左、右焦点分别为F1 , F2 , 上顶点为B,若△BF1F2的周长为6,且点F1到直线BF2的距离为b. (Ⅰ)求椭圆C的方程;
(Ⅱ)设A1 , A2是椭圆C长轴的两个端点,点P是椭圆C上不同于A1 , A2的任意一点,直线A1P交直线x=m于点M,若以MP为直径的圆过点A2 , 求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在六面体ABCD﹣A1B1C1D1中,M,N分别是棱A1B1 , B1C1的中点,平面ABCD⊥平面A1B1BA,平面ABCD平面B1BCC1 . 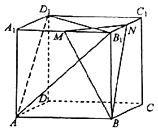
(1)证明:BB1⊥平面ABCD;
(2)已知六面体ABCD﹣A1B1C1D1的棱长均为 ![]() ,cos∠BAD=
,cos∠BAD= ![]() ,设平面BMN与平面AB1D1相交所成二面角的大小为θ求cosθ.
,设平面BMN与平面AB1D1相交所成二面角的大小为θ求cosθ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空间几何体ABCDEF如图所示.已知面ABCD⊥面ADEF,ABCD为梯形,ADEF为正方形,且AB∥CD,AB⊥AD,CD=4,AB=AD=2,G为CE的中点. (Ⅰ)求证:BG∥面ADEF;
(Ⅱ)求证:面DBG⊥面BDF.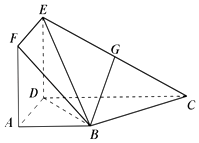
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李冶(1192﹣1279),真定栾城(今属河北石家庄市)人,金元时期的数学家、诗人、晚年在封龙山隐居讲学,数学著作多部,其中《益古演段》主要研究平面图形问题:求圆的直径,正方形的边长等,其中一问:现有正方形方田一块,内部有一个圆形水池,其中水池的边缘与方田四边之间的面积为13.75亩,若方田的四边到水池的最近距离均为二十步,则圆池直径和方田的边长分别是(注:240平方步为1亩,圆周率按3近似计算)( )
A.10步、50步
B.20步、60步
C.30步、70步
D.40步、80步
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x2﹣x﹣1)ex .
(1)求函数f(x)的单调区间.
(2)若方程a( ![]() +1)+ex=ex在(0,1)内有解,求实数a的取值范围.
+1)+ex=ex在(0,1)内有解,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com