练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】选修4-4：坐标系与参数方程

    已知直线的参数方程为（为参数， ），以坐标原点为极点， 轴正半轴为极轴建立极坐标系，圆的极坐标方程为.

    （Ⅰ）讨论直线与圆的公共点个数；

    （Ⅱ）过极点作直线的垂线，垂足为，求点的轨迹与圆相交所得弦长.

    【答案】（Ⅰ）见解析；（Ⅱ）点的轨迹与圆相交所得弦长是.

    【解析】试题分析： (Ⅰ)根据直线参数方程的几何意义可知直线式过定点，将极坐标方程化为直角坐标，可知圆心为 ，半径为 ，动态讨论倾斜角可得结果；(Ⅱ)直线与圆的极坐标方程联立，求出极径，即可得结果.

    试题解析：(Ⅰ)直线式过定点，倾斜角在内的一条直线，

    圆的方程为，∴当时，直线与圆有1个公共点；

    当时，直线与圆有2个公共点

    (Ⅱ)依题意，点在以为直径的圆上，可得轨迹极坐标方程为.

    联立得.

    ∴点的轨迹与圆相交所得弦长是.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设直线l的方程为(a＋1)x＋y＋2－a＝0(a∈R)．

    （Ⅰ）若直线l不经过第二象限，求实数a的取值范围；

    （Ⅱ)若直线l与两坐标轴围成的三角形面积等于2，求实数a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（）.

    （Ⅰ）若，当时，求的单调递减区间；

    （Ⅱ）若函数有唯一的零点，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在边长为4的正方形的边上有一点沿着折线由点(起点）向点(终点）运动。设点运动的路程为，的面积为，且与之间的函数关系式用如图所示的程序框图给出.

    （1）写出框图中①、②、③处应填充的式子；

    （2）若输出的面积值为6，则路程的值为多少？并指出此时点在正方形的什么位置上？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】等比数列{an}的各项均为正数，且2a1+3a2=1，a32=9a2a6 ，
    （1）求数列{an}的通项公式；
    （2）设bn=log3a1+log3a2+…+log3an ， 求数列{ }的前n项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，a、b、c分别是角A、B、C的对边，且 ，
    （1）求角B的大小；
    （2）若 ，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】矩形ABCD的两条对角线相交于点M(2,0)，AB边所在直线的方程为x－3y－6＝0，点T(－1,1)在AD边所在直线上．

    （1）求AD边所在直线的方程；

    （2）求矩形ABCD外接圆的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四凌锥S﹣ABCD中，底面ABCD是直角梯形，AD∥BC，SA⊥CD，AB⊥平面SAD，M是SC的中点，且SA=AB=BC=2，AD=1．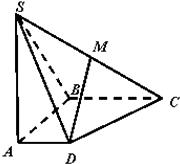

    （1）求证：DM∥平面SAB；
    （2）求四棱锥S﹣ABCD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数列{an}中，an=32，sn=63，
    （1）若数列{an}为公差为11的等差数列，求a1；
    （2）若数列{an}为以a1=1为首项的等比数列，求数列{am2}的前m项和sm′ ．

    查看答案和解析>>

    同步练习册答案