
| 成绩等级 | A | B | C | D | E |
| 成绩(分) | 90 | 70 | 60 | 40 | 30 |
| 人数(名) | 4 | 6 | 10 | 7 | 3 |
 =
= ,
, .
.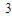 (
( )(
)( )3=
)3=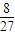 ;P(X=1)=C
;P(X=1)=C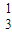 (
( )1(
)1( )2=
)2= ;
;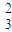 (
( )2(
)2( )=
)= ;
;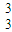 (
( )3(
)3( )=
)=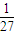 ;
;| X | 1 | 2 | 3 | |
| P | 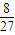 |  |  |  |
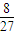 +1×
+1× +2×
+2× +3×
+3×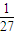 =1,所求期望值为1.
=1,所求期望值为1.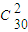 ,
,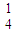 (C
(C +C
+C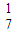 +C
+C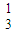 );
);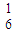 (C
(C +C
+C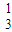 );
);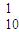 C
C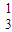 ;
;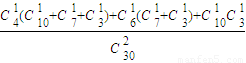 =
=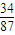 .
.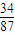 .
.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
| 成绩等级 | A | B | C | D | E |
| 成绩(分) | 90 | 70 | 60 | 40 | 30 |
| 人数(名) | 4 | 6 | 10 | 7 | 3 |
查看答案和解析>>
科目:高中数学 来源:河北省冀州市中学2012届高三第一次仿真考试数学理科试题 题型:044
某学校为了增强学生对数学史的了解,提高学生学习数学的积极性,举行了一次数学数学史知识竞赛,其中一道题是连线题,要求将4名不同的数学家与他们所著的4本不同的著作一对一连线,每连对一条得5分,连错扣2分.有一位参赛者随机用4条线把数学家与著作一对一全部连接起来.
(Ⅰ)求该参赛者恰好连对一条的概率;
(Ⅱ)设X为该参赛者此题的得分,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 成绩等级 | A | B | C | D | E |
| 成绩(分) | 90 | 70 | 60 | 40 | 30 |
| 人数(名) | 4 | 6 | 10 | 7 | 3 |
查看答案和解析>>
科目:高中数学 来源:朝阳区二模 题型:解答题
| 成绩等级 | A | B | C | D | E |
| 成绩(分) | 90 | 70 | 60 | 40 | 30 |
| 人数(名) | 4 | 6 | 10 | 7 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com