
分析 (1)由条件利用同角三角函数的基本关系,求得要求式子的值.
(2)利用诱导公式,两角差的三角公式,化简要求式子,可得结果.
解答 解:(1)∵已知$tanα=\sqrt{2}$,∴1+sin2α+cos2α=$\frac{{sin}^{2}α+2sinαcosα+{2cos}^{2}α}{{sin}^{2}α{+cos}^{2}α}$
=$\frac{{tan}^{2}α+tanα+2}{{tan}^{2}α+1}$=$\frac{4+\sqrt{2}}{3}$.
(2)$\frac{{2sin{{50}°}+sin{{80}°}(1+\sqrt{3}tan{{10}°})}}{{\sqrt{1+sin{{100}°}}}}$=$\frac{2sin50°+cos10°•\frac{cos10°+\sqrt{3}sin10°}{cos10°}}{\sqrt{{(sin50°+cos50°)}^{2}}}$
=$\frac{2sin50°+2(\frac{1}{2}cos10°+\frac{\sqrt{3}}{2}sin10°)}{sin50°+cos50°}$=$\frac{2sin50°+2sin40°}{sin50°+cos50°}$=$\frac{2sin50°+2cos50°}{sin50°+cos50°}$=2,
点评 本题主要考查同角三角函数的基本关系,诱导公式,两角差的三角公式的应用,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 图象关于$x=\frac{π}{3}$对称 | |
| B. | 图象关于$(\frac{2π}{3},0)$对称 | |
| C. | 在$[\frac{2π}{3},\frac{8π}{3}]$上单调递减 | |
| D. | 单调递增区间是$[2kπ-\frac{4π}{3},2kπ+\frac{2π}{3}](k∈Z)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
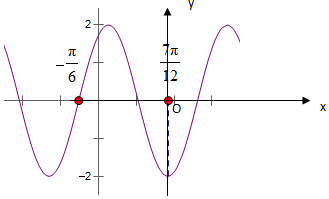 已知f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的图象如图所示.
已知f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 年产量/亩 | 年种植成本/亩 | 每吨售价 | |
| 黄瓜 | 4吨 | 1.2万元 | 0.55万元 |
| 冬瓜 | 6吨 | 0.9万元 | 0.3万元 |
| A. | 50,0 | B. | 30,20 | C. | 20,30 | D. | 0,50 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {1} | C. | {0,1,2} | D. | {2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -1 | C. | -1或3 | D. | 0 或 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com