
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间及极值;
的单调区间及极值;
(2)设![]() 时,存在
时,存在![]() ,使方程
,使方程![]() 成立,求实数
成立,求实数![]() 的最小值.
的最小值.
科目:高中数学 来源: 题型:
【题目】设各项均为正数的数列{an}的前n项和为Sn,满足:对任意的n∈N*,都有an+1+Sn+1=1,又a1![]() .
.
(1)求数列{an}的通项公式;
(2)令bn=log2an,求![]() (n∈N*)
(n∈N*)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过原点的动直线l与圆![]() 相交于不同的两点A,B.
相交于不同的两点A,B.
(1)求线段AB的中点M的轨迹C的方程;
(2)是否存在实数k,使得直线L:y=k(x﹣4)与曲线C只有一个交点?若存在,求出k的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 交于
交于![]() 两点,点
两点,点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
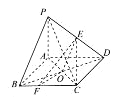
【题目】如图所示,底面为正方形的四棱锥P-ABCD中,AB=2,PA=4,PB=PD=![]() ,AC与BD相交于点O,E为PD中点.
,AC与BD相交于点O,E为PD中点.
(1)求证:EO//平面PBC;
(2)设线段BC上点F满足CF=2BF,求锐二面角E-OF-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】苹果是人们日常生活中常见的营养型水果.某地水果批发市场销售来自5个不同产地的富士苹果,各产地的包装规格相同,它们的批发价格(元/箱)和市场份额如下:
产地 |
|
|
|
|
|
批发价格 |
|
|
|
|
|
市场份额 |
|
|
|
|
|
市场份额亦称“市场占有率”.指某一产品的销售量在市场同类产品中所占比重.
(1)从该地批发市场销售的富士苹果中随机抽取一箱,求该箱苹果价格低于![]() 元的概率;
元的概率;
(2)按市场份额进行分层抽样,随机抽取![]() 箱富士苹果进行检验,
箱富士苹果进行检验,
①从产地![]() 共抽取
共抽取![]() 箱,求
箱,求![]() 的值;
的值;
②从这![]() 箱苹果中随机抽取两箱进行等级检验,求两箱产地不同的概率;
箱苹果中随机抽取两箱进行等级检验,求两箱产地不同的概率;
(3)由于受种植规模和苹果品质的影响,预计明年产地![]() 的市场份额将增加
的市场份额将增加![]() ,产地
,产地![]() 的市场份额将减少
的市场份额将减少![]() ,其它产地的市场份额不变,苹果销售价格也不变(不考虑其它因素).设今年苹果的平均批发价为每箱
,其它产地的市场份额不变,苹果销售价格也不变(不考虑其它因素).设今年苹果的平均批发价为每箱![]() 元,明年苹果的平均批发价为每箱
元,明年苹果的平均批发价为每箱![]() 元,比较
元,比较![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是通过某城市开发区中心O的两条南北和东西走向的街道,连结M,N两地之间的铁路线是圆心在
是通过某城市开发区中心O的两条南北和东西走向的街道,连结M,N两地之间的铁路线是圆心在![]() 上的一段圆弧,若点M在点O正北方向3公里;点N到的
上的一段圆弧,若点M在点O正北方向3公里;点N到的![]() 距离分别为4公里和5公里.
距离分别为4公里和5公里.
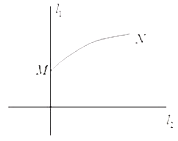
(1)建立适当的坐标系,求铁路线所在圆弧的方程;
(2)若该城市的某中学拟在点O的正东方向选址建分校,考虑环境问题,要求校址到点O的距离大于4公里,并且铁路上任意一点到校址的距离不能小于![]() 公里,求该校址距点O的最短距离(注:校址视为一个点)
公里,求该校址距点O的最短距离(注:校址视为一个点)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com