分析:(Ⅰ)依题意,由程序框图即可写出数列{an}的一个递推关系式;a1=a2=1,
(Ⅱ)令an+2-man+1=p(an+1-an),依题意可求得m=3,p=2,利用等比数列的定义可证:{an+1-3an}是等比数列;利用累加法可求出{an}的通项公式;
(Ⅲ)由(Ⅱ)知an=2n-3n-1,利用错位相减法即可求得Tn.
解答:解:(Ⅰ)依题意,a
1=a
2=1,a
n+2=5a
n+1-6a
n;
(Ⅱ)令a
n+2-ma
n+1=p(a
n+1-ma
n),则
,
解得m=3,p=2或m=2,p=3.
取m=3,p=2,则
=2,又a
2-3a
1=1-3=-2,
∴{a
n+1-3a
n}是以-2为首项,2为公比的等比数列,
∴a
n+1-3a
n=(-2)•2
n-1=-2
n.
∴
-
=-
•
()n.
∴
-
=-
•
()n-1,
…
-
=-
•
()1,
∴
-
=-
[
()1+
()2+…+
()n-1]=-
×2[1-
()n-1]=-
+
()n.
∴
=-
+
()n,
∴a
n=2
n-3
n-1.
(Ⅲ)∵a
n=2
n-3
n-1,
∴a
n+3
n-1=2
n,
∴T
n=1×2+2×2
2+3×2
3+…+n×2
n,①
2T
n=1×2
2+2×2
3+…+(n-1)×2
n+n×2
n+1,②
①-②得:-T
n=2+2
2+2
3+…+2
n-n×2
n+1=
-n×2
n+1=2
n+1(1-n)-2,
∴T
n=(n-1)•2
n+1+2.
点评:本题考查数列求和,着重考查等比关系的确定,突出考查累加法与错位相减法求和,考查转化思想与创新能力,求{an}的通项公式是难点,属于难题.

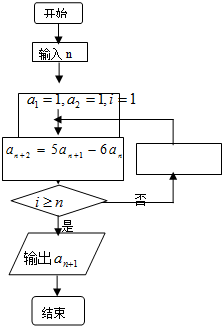 已知数列{an}满足如图所示的流程图
已知数列{an}满足如图所示的流程图
