
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为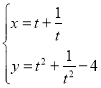 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的普通方程;
的普通方程;
(2)以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,(
,(![]() ),直线
),直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求线段
两点,求线段![]() 的长度
的长度![]() .
.
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,点
,点![]() 为曲线
为曲线![]() 上的动点,求线段
上的动点,求线段![]() 的中点
的中点![]() 到直线
到直线![]() 的距离的最大值.并求此时点
的距离的最大值.并求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿波罗尼斯(古希腊数学家,约公元前262-190年)的著作《圆锥曲线论》是古代世界光辉的科学成果,它将圆锥曲线的性质网罗殆尽,几乎使后人没有插足的余地.他证明过这样一个命题:平面内与两定点距离的比为常数![]() 的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.①若定点为
的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.①若定点为![]() ,写出
,写出![]() 的一个阿波罗尼斯圆的标准方程__________;②△
的一个阿波罗尼斯圆的标准方程__________;②△![]() 中,
中,![]() ,则当△
,则当△![]() 面积的最大值为
面积的最大值为![]() 时,
时,![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线l的参数方程为
中,直线l的参数方程为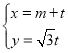 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和C的直角坐标方程;
的普通方程和C的直角坐标方程;
(2)直线![]() 上的点
上的点![]() 为曲线
为曲线![]() 内的点,且直线
内的点,且直线![]() 与曲线
与曲线![]() 交于
交于![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直四棱柱![]() 中,底面
中,底面![]() 是边长为6的正方形,点
是边长为6的正方形,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() ,过点
,过点![]() 作直四棱柱
作直四棱柱![]() 外接球的截面,所得的截面面积的最大值与最小值之差为
外接球的截面,所得的截面面积的最大值与最小值之差为![]() ,则直四棱柱
,则直四棱柱![]() 外接球的半径为( )
外接球的半径为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
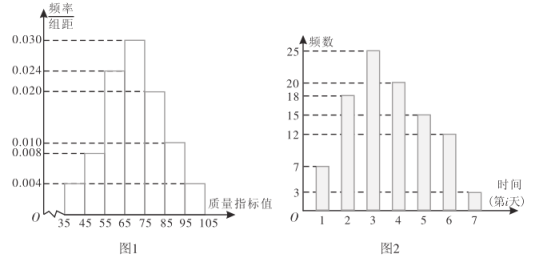
【题目】某工厂的一台某型号机器有2种工作状态:正常状态和故障状态.若机器处于故障状态,则停机检修.为了检查机器工作状态是否正常,工厂随机统计了该机器以往正常工作状态下生产的1000个产品的质量指标值,得出如图1所示频率分布直方图.由统计结果可以认为,这种产品的质量指标值服从正态分布![]() ,其中
,其中![]() 近似为这1000个产品的质量指标值的平均数
近似为这1000个产品的质量指标值的平均数![]() ,
,![]() 近似为这1000个产品的质量指标值的方差
近似为这1000个产品的质量指标值的方差![]() (同一组中的数据用该组区间中点值为代表).若产品的质量指标值全部在
(同一组中的数据用该组区间中点值为代表).若产品的质量指标值全部在![]() 之内,就认为机器处于正常状态,否则,认为机器处于故障状态.
之内,就认为机器处于正常状态,否则,认为机器处于故障状态.
(1)下面是检验员在一天内从该机器生产的产品中随机抽取10件测得的质量指标值:
29 45 55 63 67 73 78 87 93 113
请判断该机器是否出现故障?
(2)若机器出现故障,有2种检修方案可供选择:
方案一:加急检修,检修公司会在当天排除故障,费用为700元;
方案二:常规检修,检修公司会在七天内的任意一天来排除故障,费用为200元.
现需决策在机器出现故障时,该工厂选择何种方案进行检修,为此搜集检修公司对该型号机器近100单常规检修在第i(![]() ,2,…,7)天检修的单数,得到如图2所示柱状图,将第i天常规检修单数的频率代替概率.已知该机器正常工作一天可收益200元,故障机器检修当天不工作,若机器出现故障,该选择哪种检修方案?
,2,…,7)天检修的单数,得到如图2所示柱状图,将第i天常规检修单数的频率代替概率.已知该机器正常工作一天可收益200元,故障机器检修当天不工作,若机器出现故障,该选择哪种检修方案?
附:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() )上的两个动点
)上的两个动点![]() 和
和![]() ,焦点为F.线段AB的中点为
,焦点为F.线段AB的中点为![]() ,且A,B两点到抛物线的焦点F的距离之和为8.
,且A,B两点到抛物线的焦点F的距离之和为8.
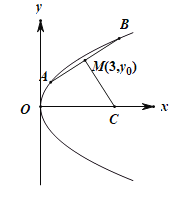
(1)求抛物线的标准方程;
(2)若线段AB的垂直平分线与x轴交于点C,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为等边三角形,
为等边三角形,![]() ,P,Q依次为AC,AB上的点,且线段PQ将
,P,Q依次为AC,AB上的点,且线段PQ将![]() 分为面积相等的两部分,设
分为面积相等的两部分,设![]() ,
,![]() ,
,![]() .
.
(1)用解析式将t表示成x的函数;
(2)用解析式将y表示成x的函数;
(3)求y的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
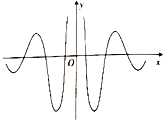
【题目】著名数学家华罗庚先生曾说过:“数缺形时少直观,形缺数时难入微数形结合百般好,隔裂分家万事休.”在数学的学习和研究中,我们经常用函数的图象来研究函数的性质,也经常用函数的解析式来琢磨函数的图象的特征,如某体育品牌的LOGO为![]() ,可抽象为如图所示的轴对称的优美曲线,下列函数中,其图象大致可“完美”局部表达这条曲线的函数是( )
,可抽象为如图所示的轴对称的优美曲线,下列函数中,其图象大致可“完美”局部表达这条曲线的函数是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com