解:(I)记“甲投篮1次投进”为事件A,“乙投篮1次投进”为事件B,“两人各投1次,恰有1人投进”为事件C,
所以P(A)=

,P(B)=

,
根据相互独立事件的概率乘法公式可得:P(C)=
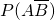
+
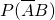
=
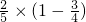
+
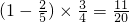
,
所以甲投进而乙未投进的概率为
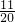
.
(Ⅱ)随机变量ξ表示乙投篮3次后投进的总次数,可能取值为0,1,2,3,则ξ~B
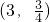
∴
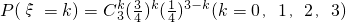
数学期望Eξ=
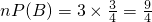
分析:(I)记“甲投篮1次投进”为事件A,“乙投篮1次投进”为事件B,“两人各投1次,恰有1人投进”为事件C,则事件C包括甲中已不中,甲不中乙中.由题意可得事件A,B是相互独立事件,进而根据相互独立事件的概率乘法公式求出答案.
(Ⅱ)随机变量ξ表示乙投篮3次后投进的总次数,可能取值为0,1,2,3,则ξ~B
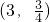
,根据二项分别的概率和期望公式可得到答案.
点评:本题以投篮为素材,考查相互独立事件的定义与计算公式,考查二项分布.解决此题的关键是首先明确事件之间的关系,即是独立关系还是相互独立关系,进而选择正确的公式进行解题.

 ,乙投进的概率为
,乙投进的概率为 ,两人投进与否要睛互没有影响.
,两人投进与否要睛互没有影响. ,P(B)=
,P(B)= ,
,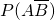 +
+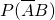 =
=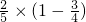 +
+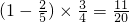 ,
,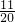 .
.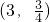
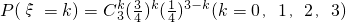
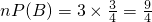
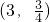 ,根据二项分别的概率和期望公式可得到答案.
,根据二项分别的概率和期望公式可得到答案.
