[题目]为了缓解城市交通压力.某市市政府在市区一主要交通干道修建高架桥.两端的桥墩现已建好.已知这两桥墩相距m米.“余下的工程只需建两端桥墩之间的桥面和桥墩．经测算.一个桥墩的工程费用为256万元,距离为x米的相邻两墩之间的桥面工程费用为(2+)x万元．假设桥墩等距离分布.所有桥墩都视为点.且不考虑其他因素．记“余下工程的费用为y 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】为了缓解城市交通压力，某市市政府在市区一主要交通干道修建高架桥，两端的桥墩现已建好，已知这两桥墩相距m米，“余下的工程”只需建两端桥墩之间的桥面和桥墩．经测算，一个桥墩的工程费用为256万元；距离为x米的相邻两墩之间的桥面工程费用为(2＋)x万元．假设桥墩等距离分布，所有桥墩都视为点，且不考虑其他因素．记“余下工程”的费用为y万元．

(1)试写出工程费用y关于x的函数关系式；

(2)当m＝640米时，需新建多少个桥墩才能使工程费用y最小？并求出其最小值．

【答案】（1）；（2）需新建9个桥墩才能使工程费用y取得最小值，且最少费用为8 704万元．

【解析】试题分析：（1）设出相邻桥墩间距米，需建桥墩个，根据题意余下工程的费用为桥墩的总费用加上相邻两墩之间的桥面工程总费用即可得到的解析式；（2）把米代入到的解析式中并求出令其等于0，然后讨论函数的增减性判断函数的最小值时的值代入中求出桥墩个数即可.

试题解析：（1）相邻桥墩间距米，需建桥墩个，则，()
（2）当米时，，，∵且时，，单调递增，时，，单调递减，∴，∴需新建桥墩个.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】设等差数列{an}的前n项和为Sn，已知(a4－1)3＋2 016(a4－1)＝1，(a2 013－1)3＋2 016·(a2 013－1)＝－1，则下列结论正确的是(　　)

A. S2 016＝－2 016，a2 013>a4

B. S2 016＝2 016，a2 013>a4

C. S2 016＝－2 016，a2 013<a4

D. S2 016＝2 016，a2 013<a4

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知p：“x0∈(－1,1)，x－x0－m＝0(m∈R)”是正确的，设实数m的取值集合为M.

(1)求集合M；

(2)设关于x的不等式(x－a)(x＋a－2)<0(a∈R)的解集为N，若“x∈M”是“x∈N”的充分条件，求实数a的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】近年来随着我国在教育利研上的投入不断加大，科学技术得到迅猛发展，国内企业的国际竞争力得到大幅提升.伴随着国内市场增速放缓，国内确实力企业纷纷进行海外布局，第二轮企业出海潮到来，如在智能手机行业，国产品牌已在赶超国外巨头，某品牌手机公司一直默默拓展海外市场，在海外共设30多个分支机构，需要国内公司外派大量70后、80后中青年员工．该企业为了解这两个年龄层员工是否愿意被外派上作的态度，按分层抽样的方式从70后利80后的员工中随机调查了100位，得到数据如下表：

	愿意被外派	不愿意被外派	合计
70后	20	20	40
80后	40	20	60
合计	60	40	100

(1)根据凋查的数据，是否有的把握认为“是否愿意被外派与年龄有关”，并说明理由；

(2)该公司参观驻海外分支机构的交流体验活动，拟安排4名参与调查的70后员工参加，70后的员工中有愿意被外派的3人和不愿意被外派的3人报名参加，现采用随机抽样方法从报名的员工中选4人，求选到愿意被外派人数不少于不愿意被外派人数的概率.

参考数据：

	0.15	0.10	0.05	0.025	0.010	0.005
	2.072	2.706	3.841	5.024	6.635	7.879

（参考公式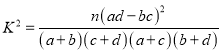：，其中）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某社区为了解辖区住户中离退休老人每天的平均户外“活动时间”，从辖区住户的离退休老人中随机抽取了100位老人进行调查，获得了每人每天的平均户外“活动时间”（单位：小时），活动时间按照、、…、从少到多分成9组，制成样本的频率分布直方图如图所示.

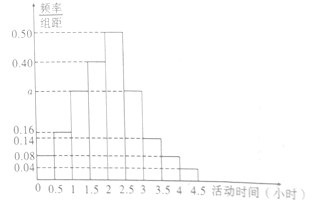
（1）求图中的值；

（2）估计该社区住户中离退休老人每天的平均户外“活动时间”的中位数；

（3）在、这两组中采用分层抽样抽取7人，再从这7人中随机抽取2人，求抽取的两人恰好都在同一个组的概率.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知椭圆的左右焦点分别为，若椭圆上一点满足，且椭圆过点，过点的直线与椭圆交于两点．

（1）求椭圆的方程；

（2）若点是点在轴上的垂足，延长交椭圆于，求证：三点共线．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知表1和表2是某年部分日期的天安门广场升旗时刻表：

表1：某年部分日期的天安门广场升旗时刻表

日期	升旗时刻	日期	升旗时刻	日期	升旗时刻	日期	升旗时刻
1月1日	7：36	4月9日	5：46	7月9日	4：53	10月8日	6：17
1月21日	7：11	4月28日	5：19	7月27日	5：07	10月26日	6：36
2月10日	7：14	5月16日	4：59	8月14日	5：24	11月13日	6：56
3月2日	6：47	6月3日	4：47	9月2日	5：42	12月1日	7：16
3月22日	6：15	6月22日	4：46	9月20日	5：50	12月20日	7：31

表2：某年1月部分日期的天安门广场升旗时刻表

日期	升旗时刻	日期	升旗时刻	日期	升旗时刻
2月1日	7：23	2月11日	7：13	2月21日	6：59
2月3日	7：22	2月13日	7：11	2月23日	6：57
2月5日	7：20	2月15日	7：08	2月25日	6：55
2月7日	7：17	2月17日	7：05	2月27日	6：52
2月9日	7：15	2月19日	7：02	2月28日	6：49