Question

【题目】在直角坐标系xOy中，直线l1的参数方程为 ，（t为参数），直线l2的参数方程为 ，（m为参数）．设l1与l2的交点为P，当k变化时，P的轨迹为曲线C．
（Ⅰ）写出C的普通方程；
（Ⅱ）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，设l3：ρ（cosθ+sinθ）﹣ =0，M为l3与C的交点，求M的极径．

Answer 1

【答案】解：（Ⅰ）∵直线l1的参数方程为 ，（t为参数），
∴消掉参数t得：直线l1的普通方程为：y=k（x﹣2）①；
又直线l2的参数方程为 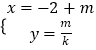，（m为参数），
同理可得，直线l2的普通方程为：x=﹣2+ky②；
联立①②，消去k得：x2﹣y2=4，即C的普通方程为x2﹣y2=4；
（Ⅱ）∵l3的极坐标方程为ρ（cosθ+sinθ）﹣ =0，
∴其普通方程为：x+y﹣ =0，
联立 得： ，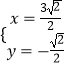
∴ρ2=x2+y2= + =5．
∴l3与C的交点M的极径为ρ= ．
【解析】解：（Ⅰ）分别消掉参数t与m可得直线l1与直线l2的普通方程为y=k（x﹣2）①与x=﹣2+ky②；联立①②，消去k可得C的普通方程为x2﹣y2=4；
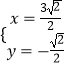（Ⅱ）将l3的极坐标方程为ρ（cosθ+sinθ）﹣ =0化为普通方程：x+y﹣ =0，再与曲线C的方程联立，可得 ，即可求得l3与C的交点M的极径为ρ= ．
【考点精析】利用极坐标系和直线的参数方程对题目进行判断即可得到答案，需要熟知平面内取一个定点O，叫做极点；自极点O引一条射线OX叫做极轴；再选定一个长度单位、一个角度单位(通常取弧度)及其正方向(通常取逆时针方向)，这样就建立了一个极坐标系；经过点，倾斜角为的直线的参数方程可表示为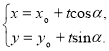（为参数）．