
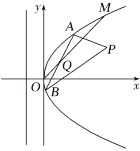
【题目】如图所示,在直角坐标系![]() 中,点
中,点![]() 到抛物线
到抛物线![]() 的准线的距离为
的准线的距离为![]() .点
.点![]() 是
是![]() 上的定点,
上的定点,![]() ,
,![]() 是
是![]() 上的两动点,且线段
上的两动点,且线段![]() 的中点
的中点![]() 在直线
在直线![]() 上.
上.
(Ⅰ)求曲线![]() 的方程及
的方程及![]() 的值;
的值;
(Ⅱ)记![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(Ⅰ)![]() ,
,![]() .(Ⅱ)
.(Ⅱ)![]() .
.
【解析】分析:(Ⅰ)由抛物线准线方程及P到准线的距离,可求得![]() ,进而求得抛物线方程,将点M的坐标代入抛物线 ,即可求得t.
,进而求得抛物线方程,将点M的坐标代入抛物线 ,即可求得t.
(Ⅱ)求直线OM方程,点Q在直线OM上,根据直线方程表示点Q坐标,消去参数n,
利用点差法表示出直线AB斜率,进而求出直线方程,将直线AB方程与抛物线方程联立,用弦长公式求弦长,从而将d表示为关于m的函数,根据m范围求最值.
详解:(1)![]() 的准线为
的准线为![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴抛物线![]() 的方程为
的方程为![]() .又点
.又点![]() 在曲线
在曲线![]() 上,∴
上,∴![]() .
.
(2)由(1)知,点![]() ,从而
,从而![]() ,即点
,即点![]() ,
,
依题意,直线![]() 的斜率存在,且不为
的斜率存在,且不为![]() ,
,
设直线![]() 的斜率为
的斜率为![]() .且
.且![]() ,
,![]() ,
,
由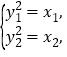 得
得![]() ,故
,故![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
由![]() 消去
消去![]() ,整理得
,整理得![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
从而![]() .
.
∴![]() ,
,
当且仅当![]() ,即
,即![]() 时,上式等号成立,
时,上式等号成立,
又![]() 满足
满足![]() .∴
.∴![]() 的最大值为
的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面CDE是等边三角形,棱![]() 。
。

(1)证明FO∥平面CDE;
(2)设BC=![]() CD,证明EO⊥平面CDE。
CD,证明EO⊥平面CDE。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗A原料1千克、B原料2千克;生产乙产品1桶需耗A原料2千克,B原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗A、B原料都不超过12千克.通过合理安排生产计划,从每天生产的甲、乙两种产品中,公司共可获得的最大利润是( )
A.1800元
B.2400元
C.2800元
D.3100元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小金同学在学校中贯彻着“边玩边学”的学风,他在“汉诺塔”的游戏中发现了数列递推的奥妙:有![]() 、
、![]() 、
、![]() 三个木桩,
三个木桩,![]() 木桩上套有编号分别为
木桩上套有编号分别为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 的七个圆环,规定每次只能将一个圆环从一个木桩移动到另一个木桩,且任意一个木桩上不能出现“编号较大的圆环在编号较小的圆环之上”的情况,现要将这七个圆环全部套到
的七个圆环,规定每次只能将一个圆环从一个木桩移动到另一个木桩,且任意一个木桩上不能出现“编号较大的圆环在编号较小的圆环之上”的情况,现要将这七个圆环全部套到![]() 木桩上,则所需的最少次数为( )
木桩上,则所需的最少次数为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂利用随机数表对生产的600个零件进行抽样测试,先将600个零件进行编号,编号分别为001,002,![]() ,599,600从中抽取60个样本,如下提供随机数表的第4行到第6行:
,599,600从中抽取60个样本,如下提供随机数表的第4行到第6行:
32 21 18 34 29 78 64 54 07 32 52 42 06 44 38 12 23 43 56 77 35 78 90 56 42
84 42 12 53 31 34 57 86 07 36 25 30 07 32 86 23 45 78 89 07 23 68 96 08 04
32 56 78 08 43 67 89 53 55 77 34 89 94 83 75 22 53 55 78 32 45 77 89 23 45
若从表中第6行第6列开始向右依次读取3个数据,则得到的第6个样本编号![]()
![]()
A. 522B. 324C. 535D. 578
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:
①函数![]() 的最小正周期是
的最小正周期是![]() ;
;
②在直角坐标系![]() 中,点
中,点![]() ,将向量
,将向量![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到向量
得到向量![]() ,则点
,则点![]() 的坐标是
的坐标是![]() ;
;
③在同一直角坐标系中,函数![]() 的图象和函数
的图象和函数![]() 的图象有两个公共点;
的图象有两个公共点;
④函数![]() 在
在![]() 上是增函数.
上是增函数.
其中,正确的命题是________(填正确命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知数列![]() 是等比数列,且公比为
是等比数列,且公比为![]() ,记
,记![]() 是数列
是数列![]() 的前
的前![]() 项和.
项和.
(1)若![]() =1,
=1,![]() >1,求
>1,求![]() 的值;
的值;
(2)若首项![]() ,
,![]() ,
,![]() 是正整数,满足不等式|
是正整数,满足不等式|![]() ﹣63|<62,且
﹣63|<62,且![]() 对于任意正整数
对于任意正整数![]() 都成立,问:这样的数列
都成立,问:这样的数列![]() 有几个?
有几个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com