
【题目】如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=![]() ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.
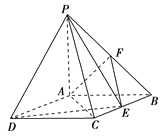
(1)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(2)求证:无论点E在BC边的何处,都有![]() ;
;
(3)当![]() 为何值时,
为何值时,![]() 与平面
与平面![]() 所成角的大小为45°.
所成角的大小为45°.
【答案】(1)EF//面PAC (2)见解析(3)![]()
【解析】
试题⑴当E是BC中点时,因F是PB的中点,所以EF为![]() 的中位线,
的中位线,
故EF//PC,又因![]() 面PAC,
面PAC,![]() 面PAC,所以EF//面PAC
面PAC,所以EF//面PAC
⑵证明:因PA⊥底面ABCD,所以DA⊥PA,又DA⊥AB,所以DA⊥面PAB,
又DA//CB,所以CB⊥面PAB,而![]() 面PAB,所以
面PAB,所以![]() ,
,
又在等腰三角形PAB中,中线AF⊥PB,PB![]() CB=B,所以AF⊥面PBC.
CB=B,所以AF⊥面PBC.
而PE![]() 面PBC,所以无论点E在BC上何处,都有
面PBC,所以无论点E在BC上何处,都有![]()
⑶以A为原点,分别以AD、AB、AP为x、y、z轴建立坐标系,设![]() ,
,
则![]() ,
,![]() ,
,![]() ,设面PDE的法向量为
,设面PDE的法向量为![]() ,
,
由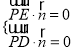 ,得
,得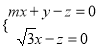 ,取
,取![]() ,又
,又![]() ,
,
则由![]() ,得
,得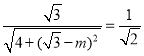 ,解得
,解得![]() .
.
故当![]() 时,PA与面PDE成
时,PA与面PDE成![]() 角
角


科目:高中数学 来源: 题型:
【题目】根据如图给出的2005年至2016年我国人口总量及增长率的统计图,以下结论不正确的是![]()
![]()
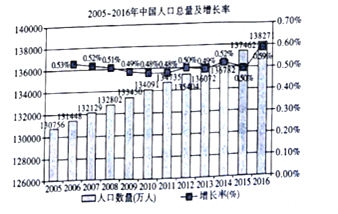
A. 自2005年以来,我国人口总量呈不断增加趋势
B. 自2005年以来,我国人口增长率维持在![]() 上下波动
上下波动
C. 从2005年后逐年比较,我国人口增长率在2016年增长幅度最大
D. 可以肯定,在2015年以后,我国人口增长率将逐年变大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若椭圆![]() 的焦点在x轴上,离心率为
的焦点在x轴上,离心率为![]() ,依次连接
,依次连接![]() 的四个顶点所得四边形的面积为40.
的四个顶点所得四边形的面积为40.
(1)试求![]() 的标准方程;
的标准方程;
(2)若曲线M上任意一点到![]() 的右焦点的距离与它到直线
的右焦点的距离与它到直线![]() 的距离相等,直线
的距离相等,直线![]() 经过
经过![]() 的下顶点和右顶点,
的下顶点和右顶点,![]() ,直线
,直线![]() 与曲线M相交于点P、Q(点P在第一象限内,点Q在第四象限内),设
与曲线M相交于点P、Q(点P在第一象限内,点Q在第四象限内),设![]() 的下顶点是B,上顶点是D,且
的下顶点是B,上顶点是D,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运动制衣品牌为了成衣尺寸更精准,现选择15名志愿者,对其身高和臂展进行测量(单位:厘米),左图为选取的15名志愿者身高与臂展的折线图,右图为身高与臂展所对应的散点图,并求得其回归方程为![]() ,以下结论中不正确的为
,以下结论中不正确的为


A. 15名志愿者身高的极差小于臂展的极差
B. 15名志愿者身高和臂展成正相关关系,
C. 可估计身高为190厘米的人臂展大约为189.65厘米,
D. 身高相差10厘米的两人臂展都相差11.6厘米,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若点
,若点![]() 在
在![]() 的图像上运动,则点
的图像上运动,则点![]() 在
在![]() 的图象上运动
的图象上运动
(1)求![]() 的最小值,及相应的
的最小值,及相应的![]() 值
值
(2)求函数![]() 的解析式,指出其定义域
的解析式,指出其定义域![]() ,判断并证明
,判断并证明![]() 在
在![]() 上的单调性
上的单调性
(3)在函数![]() 和
和![]() 的图象上是否分别存在点
的图象上是否分别存在点![]() 关于直线
关于直线![]() 对称,若存在,求出点
对称,若存在,求出点![]() 的坐标;若不存在,请说明理由
的坐标;若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的值域为A,
的值域为A,![]() .
.
(1)当![]() 的为偶函数时,求
的为偶函数时,求![]() 的值;
的值;
(2) 当![]() 时,
时, ![]() 在A上是单调递增函数,求
在A上是单调递增函数,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,(其中
时,(其中![]() ),若
),若![]() ,且函数
,且函数![]() 的图象关于点
的图象关于点![]() 对称,在
对称,在![]() 处取 得最小值,试探讨
处取 得最小值,试探讨![]() 应该满足的条件.
应该满足的条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学习小组在研究性学习中,对昼夜温差大小与绿豆种子一天内出芽数之间的关系进行研究该小组在4月份记录了1日至6日每天昼夜最高、最低温度(如图1),以及浸泡的100颗绿豆种子当天内的出芽数(如图2).
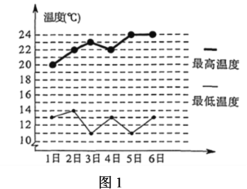
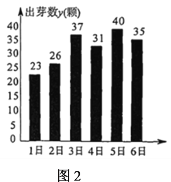
根据上述数据作出散点图,可知绿豆种子出芽数(颗)和温差具有线性相关关系.
附: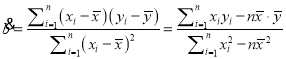 ,
,![]()
(1)求绿豆种子出芽数(颗)关于温差的回归方程;
(2)假如4月1日至7日的日温差的平均值为11℃,估计4月7日浸泡的10000颗绿豆种子一天内的出芽数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某经销商从某养殖场购进某品种河蟹,并随机抽取了 100只进行统计,按重量分类统计,得到频率分布直方图如下:
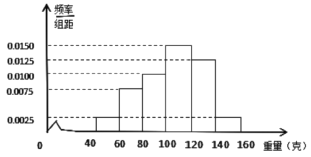
(1)记事件![]() 为“从这批河蟹中任取一只,重量不超过120克”,估计
为“从这批河蟹中任取一只,重量不超过120克”,估计![]() ;
;
(2)试估计这批河蟹的平均重量;
(3)该经销商按有关规定将该品种河蟹分三个等级,并制定出销售单价如下:
等级 | 特级 | 一级 | 二级 |
重量 |
|
|
|
单价(元/只) | 40 | 20 | 10 |
试估算该经销商以每千克至多花多少元(取整)收购这批河蟹,才能获利?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com