在各项均为正数的数列{an}中,前n项和Sn满足2Sn+1=an(2an+1),n∈N*.
(1)证明{an}是等差数列,并求这个数列的通项公式及前n项和的公式;
(2)在平面直角坐标系xoy面上,设点Mn(xn,yn)满足an=nxn,Sn=n2yn,且点Mn在直线l上,Mn中最高点为Mk,若称直线l与x轴.直线x=a,x=b所围成的图形的面积为直线l在区间[a,b]上的面积,试求直线l在区间[x3,xk]上的面积;
(3)若存在圆心在直线l上的圆纸片能覆盖住点列Mn中任何一个点,求该圆纸片最小面积.
【答案】
分析:本题是解析几何、数列、极限多知识点融合一体的综合性题,重点考查数列中a
n和S
n的关系、等差数列的证明、求数列的通项公式、前n项和、直线方程的应用、极限的思想等;
(1)该小题较易,利用a
n=s
n-s
n-1就可以把已知条件转化为关于a
n的递推关系,进而得到{a
n}为等差数列,其通项公式、前n项和易得;
(2)根据题意可得点M
n(

+

,

),令x=

,y=

,消去n得关于x、y的方程,再根据y=

是n的减函数可得M
1为M
n中的最高点,且M
1(1,1),又满足条件的图形为直角梯形,从而求得其面积;
(3)根据直线C:3x-2y-1=0上的点列M
n依次为M
1(1,1),M
2(

,

),M
3(

,

),…,M
n(

,

),可得其极限点M(

,

),从而|M
1M|,最小圆纸片的面积即得.
解答:解:(1)由已知得2S
n=2a
n2+a
n-1①
故2S
n+1=2a
n+12+a
n+1-1②
②-①得2a
n+1=2a
n+12-2a
n2+a
n+1-a
n结合a
n>0,得a
n+1-a
n=

∴{a
n}是等差数列
又n=1时,2a
1=a
12+a
1-1,解得a
1=1或a
1=

∵a
n>0,∴a
1=1
又d=

,故a
n=1+

(n-1)=

n+

∴S
n=n+

=

n
2+

n;
(2)∵a
n=nx
n,S
n=n
2y
n∴x
n=

=

+

,y
n=
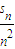
=

+

即得点M
n(

+

,
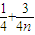
)
设x=
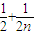
,y=

,
消去n,得3x-2y-1=0,
即直线C的方程为3x-2y-1=0
又y=

是n的减函数
∴M
1为M
n中的最高点,且M
1(1,1)
又M
3的坐标为(

,

)
∴C与x轴.直线x=

,x=1围成的图形为直角梯形
从而直线C在[

,1]上的面积为
S=

×(

+1)×(1-

)=

;(9分)
(3)由于直线C:3x-2y-1=0上的点列M
n依次为
M
1(1,1),M
2(

,

),M
3(

,

),
M
n(

,

),
而

(

)=

,

(

)=

因此,点列M
n沿直线C无限接近于极限点M(

,

)
又

|M
1M|=


=
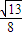
所以最小圆纸片的面积为

.
点评:本题题型大,覆盖面广,应用知识丰富,是一个难度大的题目;要正确的解好本题,不仅具备全面的知识方法,还需要一定的耐力,有时解题的意志力也是决定题目是否解出的重要因素,本题的解答就是一个很好的例证;所以解题过程中,不仅积累知识和方法,还是培养人的耐心的方式,是对人的心理因素的考验.

 +
+ ,
, ),令x=
),令x= ,y=
,y= ,消去n得关于x、y的方程,再根据y=
,消去n得关于x、y的方程,再根据y= 是n的减函数可得M1为Mn中的最高点,且M1(1,1),又满足条件的图形为直角梯形,从而求得其面积;
是n的减函数可得M1为Mn中的最高点,且M1(1,1),又满足条件的图形为直角梯形,从而求得其面积; ,
, ),M3(
),M3( ,
, ),…,Mn(
),…,Mn( ,
, ),可得其极限点M(
),可得其极限点M( ,
, ),从而|M1M|,最小圆纸片的面积即得.
),从而|M1M|,最小圆纸片的面积即得.

 ,故an=1+
,故an=1+ (n-1)=
(n-1)= n+
n+
 =
= n2+
n2+ n;
n; =
= +
+ ,yn=
,yn=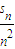 =
= +
+
 +
+ ,
,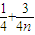 )
)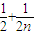 ,y=
,y= ,
, 是n的减函数
是n的减函数 ,
, )
) ,x=1围成的图形为直角梯形
,x=1围成的图形为直角梯形 ,1]上的面积为
,1]上的面积为 ×(
×( +1)×(1-
+1)×(1- )=
)= ;(9分)
;(9分) ,
, ),M3(
),M3( ,
, ),
), ,
, ),
), (
( )=
)= ,
, (
( )=
)=
 ,
, )
) |M1M|=
|M1M|=
 =
=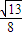
 .
.

 阅读快车系列答案
阅读快车系列答案