
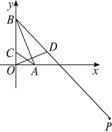
已知点A(2,0),B(0,6),O为坐标原点,
(1)若点C在线段OB上,且∠BAC=![]() ,求△ABC的面积;
,求△ABC的面积;
(2)若原点O关于直线AB的对称点为D,延长BD到P,且|PD|=2|BD|,已知直线l:ax+10y+84-108![]() =0经过点P,求直线l的倾斜角.
=0经过点P,求直线l的倾斜角.
直线l的倾斜角为![]() .
.
(1)要求△ABC的面积,关键是求C点的坐标,可利用夹角公式先求直线AC的斜率,再写出直线AC的方程,从而可求出C点坐标.
kAB=-3,
由tan![]() =
=![]() 得kAC=
得kAC=![]() .所以AC:y=
.所以AC:y=![]() (x-2).
(x-2).
令x=0,得y=1,则C(0,1),
所以S△ABC=![]() |BC|·|OA|=
|BC|·|OA|=![]() ×5×2=5.
×5×2=5.
(2)要求直线l的倾斜角,需求参数a的值.由直线l过点P,所以需求出P点的坐标,又P是BD的定比分点,所以还需由对称性求出D点的坐标.
设D点坐标为(x0,y0),
因为AB:![]() ,即3x+y-6=0,
,即3x+y-6=0,
所以 即
即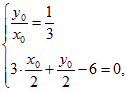 所以D(
所以D(![]() ,
,![]() ).
).
由|PD|=2|BD|,得![]() .
.
所以
将点P(![]() ,
,![]() )代入l的方程,得a=10
)代入l的方程,得a=10![]() .所以k l= -
.所以k l= -![]() .
.
故直线l的倾斜角为![]() .
.


科目:高中数学 来源: 题型:
(本小题满分12分)已知点A(2,0),B(0,6),O为坐标原点
(1)若点C在线段OB上,且∠BAC=45°,求△ABC的面积.
(2)若原点O关于直线AB的对称点为D,延长BD到P,且|PD|=2|BD|,求P点的坐标。
(3)已知直线L:ax+10y+84-108![]() =0经过P点,求直线L的倾斜角.
=0经过P点,求直线L的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)若点C在线段OB上,且∠BAC=![]() ,求△ABC的面积;
,求△ABC的面积;
(2)若原点O关于直线AB的对称点为D,延长BD到P,且|PD|=2|BD|,又直线l:ax+10y+84-108![]() =0经过点P,求直线l的倾斜角.
=0经过点P,求直线l的倾斜角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com