
【题目】如图,四边形![]() 是矩形,
是矩形, ![]() 是
是![]() 的中点,
的中点, ![]() 与
与![]() 交于点
交于点![]() 平面
平面![]() .
.
(I)求证: ![]() 面
面![]() ;
;
(II)若![]() ,求点
,求点![]() 到平面
到平面![]() 距离.
距离.
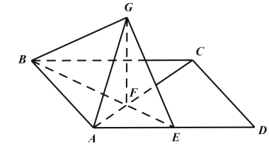
【答案】(1)见解析;(II) ![]() .
.
【解析】试题分析:(1)由相似三角形利用勾股定理证明![]() ,根据线面垂直的性质可证明
,根据线面垂直的性质可证明![]() ,再利用线面垂直的判定定理可证明
,再利用线面垂直的判定定理可证明![]() 平面
平面![]() ;(2)先根据勾股定理求出,
;(2)先根据勾股定理求出, ![]() 的值,从而可得
的值,从而可得![]() 的面积,设点
的面积,设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,利用
,利用 ![]() ,求解即可.
,求解即可.
试题解析:(I)证法1:
∵四边形![]() 为矩形,
为矩形, ![]() ,
,
![]()
又∵矩形![]() 中,
中, ![]()
在![]() 中,
中, ![]()
![]()
在![]() 中,
中, 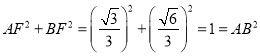
![]() ,即
,即![]()
![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
![]()
又![]() 平面
平面![]()
![]() 平面
平面![]()
(II)在![]() 中,
中, 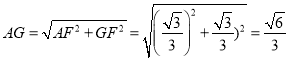
在![]() 中,
中, 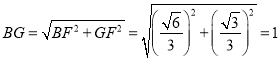
在![]() 中,
中, ![]()
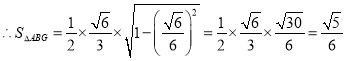
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则
,则
![]() ,
,
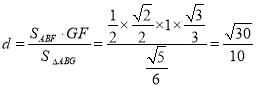
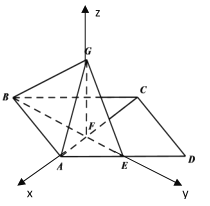
证法2;( 坐标法 )由(I)得![]() 两两垂直,以点
两两垂直,以点![]() 为原点,
为原点, ![]() 所在直线分别为
所在直线分别为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
则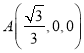 ,
, 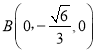 ,
, 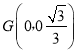 ,
,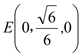
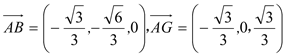 ,
,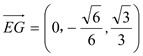 ,
,
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则
![]() ,即
,即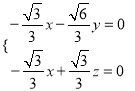 ,
,
取![]() ,得
,得![]()
设点![]() 与平面
与平面![]() 的距离为
的距离为![]() ,则
,则
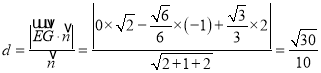
∴直线![]() 与平面
与平面![]() 的距离为
的距离为![]() .
.


科目:高中数学 来源: 题型:
【题目】将向量![]() =(
=(![]() ,
, ![]() ),
), ![]() =(
=(![]() ,
, ![]() ),…
),…![]() =(
=(![]() ,
,![]() )组成的系列称为向量列{
)组成的系列称为向量列{![]() },并定义向量列{
},并定义向量列{![]() }的前
}的前![]() 项和
项和![]() .如果一个向量列从第二项起,每一项与前一项的差都等于同一个向量,那么称这样的向量列为等差向量列。若向量列{
.如果一个向量列从第二项起,每一项与前一项的差都等于同一个向量,那么称这样的向量列为等差向量列。若向量列{![]() }是等差向量列,那么下述四个向量中,与
}是等差向量列,那么下述四个向量中,与![]() 一定平行的向量是 ( )
一定平行的向量是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
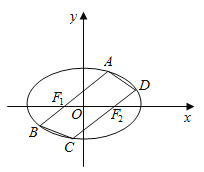
【题目】如图所示,椭圆E的中心为坐标原点,焦点![]() 在
在![]() 轴上,且
轴上,且![]() 在抛物线
在抛物线![]() 的准线上,点
的准线上,点![]() 是椭圆E上的一个动点,
是椭圆E上的一个动点, ![]() 面积的最大值为
面积的最大值为![]() .
.
(Ⅰ)求椭圆E的方程;
(Ⅱ)过焦点![]() 作两条平行直线分别交椭圆E于
作两条平行直线分别交椭圆E于![]() 四个点.
四个点.
①试判断四边形![]() 能否是菱形,并说明理由;
能否是菱形,并说明理由;
②求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
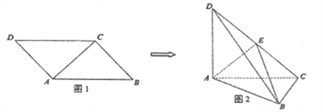
【题目】图1,平行四边形![]() 中,
中, ![]() ,
, ![]() ,现将
,现将![]() 沿
沿![]() 折起,得到三棱锥
折起,得到三棱锥![]() (如图2),且
(如图2),且![]() ,点
,点![]() 为侧棱
为侧棱![]() 的中点.
的中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积;
的体积;
(3)在![]() 的角平分线上是否存在点
的角平分线上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天气预报是气象专家根据预测的气象资料和专家们的实际经验,经过分析推断得到的,在现实的生产生活中有着重要的意义.某快餐企业的营销部门经过对数据分析发现,企业经营情况与降雨天数和降雨量的大小有关.
(Ⅰ)天气预报说,在今后的四天中,每一天降雨的概率均为![]() ,求四天中至少有两天降雨的概率;
,求四天中至少有两天降雨的概率;
(Ⅱ)经过数据分析,一天内降雨量的大小![]() (单位:毫米)与其出售的快餐份数
(单位:毫米)与其出售的快餐份数![]() 成线性相关关系,该营销部门统计了降雨量与出售的快餐份数的数据如下:
成线性相关关系,该营销部门统计了降雨量与出售的快餐份数的数据如下:
降雨量(毫米) | 1 | 2 | 3 | 4 | 5 |
快餐数(份) | 50 | 85 | 115 | 140 | 160 |
试建立![]() 关于
关于![]() 的回归方程,为尽量满足顾客要求又不造成过多浪费,预测降雨量为6毫米时需要准备的快餐份数.(结果四舍五入保留整数)
的回归方程,为尽量满足顾客要求又不造成过多浪费,预测降雨量为6毫米时需要准备的快餐份数.(结果四舍五入保留整数)
附注:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
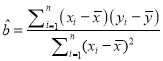 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|﹣1≤x<3},B={x|2x﹣4≥x﹣2}.
(1)求U(A∩B);
(2)若集合C={x|2x+a>0},满足B∪C=C,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
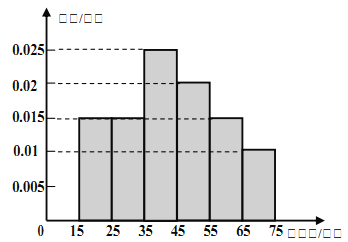
【题目】2016年5月20日,针对部分“二线城市”房价上涨过快,媒体认为国务院常务会议可能再次确定五条措施(简称“国五条”).为此,记者对某城市的工薪阶层关于“国五条”态度进行了调查,随机抽取了![]() 人,作出了他们的月收入的频率分布直方图(如图),同时得到了他们的月收入情况与“国五条”赞成人数统计表(如下表):
人,作出了他们的月收入的频率分布直方图(如图),同时得到了他们的月收入情况与“国五条”赞成人数统计表(如下表):
月收入(百元) | 赞成人数 |
|
|
|
|
|
|
|
|
|
|
|
|
(1)试根据频率分布直方图估计这![]() 人的中位数和平均月收入;
人的中位数和平均月收入;
(2)若从月收入(单位:百元)在![]() 的被调查者中随机选取
的被调查者中随机选取![]() 人进行追踪调查,求被选取的
人进行追踪调查,求被选取的![]() 人都不赞成的概率.
人都不赞成的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长方体ABCD﹣A1B1C1D1中,AB=2,AA1=AD=4,点E为AB中点.
(1)求证:BD1∥平面A1DE;
(2)求证:A1D⊥平面ABD1 . 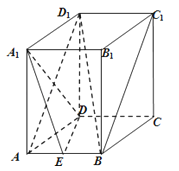
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com