
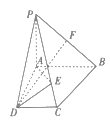
【题目】在如图所示的几何体中,面CDEF为正方形,平面ABCD为等腰梯形,AB//CD,AB =2BC,点Q为AE的中点.

(1)求证:AC//平面DQF;
(2)若∠ABC=60°,AC⊥FB,求BC与平面DQF所成角的正弦值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD为直角梯形,
中,底面ABCD为直角梯形,![]()
![]() ,
,![]() 平面ABCD,E是棱PC上的一点.
平面ABCD,E是棱PC上的一点.
(1)证明:平面![]() 平面
平面![]() .
.
(2)若![]() ,F是PB的中点,
,F是PB的中点,![]() ,
,![]() ,求直线DF与平面
,求直线DF与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现给出两个条件:①![]() ,②
,②![]() ,从中选出一个条件补充在下面的问题中,并以此为依据求解问题:(选出一种可行的条件解答,若两个都选,则按第一个解答计分)在
,从中选出一个条件补充在下面的问题中,并以此为依据求解问题:(选出一种可行的条件解答,若两个都选,则按第一个解答计分)在![]() 中,
中,![]() 分别为内角
分别为内角![]() 所对的边( ).
所对的边( ).
(1)求![]() ;
;
(2)若![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系x0y中,把曲线![]()
![]() α为参数)上每个点的横坐标变为原来的
α为参数)上每个点的横坐标变为原来的![]() 倍,纵坐标不变,得到曲线
倍,纵坐标不变,得到曲线![]() 以坐标原点为极点,以x轴正半轴为极轴,建立极坐标系,曲线
以坐标原点为极点,以x轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程
的极坐标方程![]()
(1)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设点M在![]() 上,点N在
上,点N在![]() 上,求|MN|的最小值以及此时M的直角坐标.
上,求|MN|的最小值以及此时M的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x|x﹣a|,a∈R.
(1)当f(2)+f(﹣2)>4时,求a的取值范围;
(2)若a>0,x,y∈(﹣∞,a],不等式f(x)≤|y+3|+|y﹣a|恒成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com