
【题目】向体积为1的正方体密闭容器内注入体积为![]() 的液体,旋转容器,下列说法正确的是( )
的液体,旋转容器,下列说法正确的是( )
A.当![]() 时,容器被液面分割而成的两个几何体完全相同
时,容器被液面分割而成的两个几何体完全相同
B.![]() ,液面都可以成正三角形形状
,液面都可以成正三角形形状
C.当液面与正方体的某条体对角线垂直时,液面面积的最大值为![]()
D.当液面恰好经过正方体的某条体对角线时,液面边界周长的最小值为![]()
 全能练考卷系列答案
全能练考卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() (
(![]() 为坐标原点)的面积为
为坐标原点)的面积为![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)如图,点![]() 为椭圆上一动点(非长轴端点)
为椭圆上一动点(非长轴端点)![]() ,
,![]() 为左、右焦点,
为左、右焦点,![]() 的延长线与椭圆交于
的延长线与椭圆交于![]() 点,
点,![]() 的延长线与椭圆交于
的延长线与椭圆交于![]() 点,求
点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“扶贫帮困”是中华民族的传统美德,某大型企业为帮扶贫困职工,设立“扶贫帮困基金”,采用如下方式进行一次募捐:在不透明的箱子中放入大小均相同的白球六个,红球三个,每位献爱心的参与者投币100元有一次摸奖机会,一次性从箱中摸球三个(摸完球后将球放回),若有一个红球,奖金20元,两个红球奖金40元,三个全为红球奖金200元.
(1)求一位献爱心参与者不能获奖的概率;
(2)若该次募捐有300位献爱心参与者,求此次募捐所得善款的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若函数![]() 在区间
在区间![]() 上单调递减,求实数a的取值范围;
上单调递减,求实数a的取值范围;
(2)当![]() ,(
,(![]() )时,求证:
)时,求证:![]() ;
;
(3)若函数![]() 有两个极值点
有两个极值点![]() ,
,![]() ,求证:
,求证:![]() (e为自然对数的底数)
(e为自然对数的底数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的个数是( )
①“x>1”是“x>2”的充分不必要条件;
②f(x)是其定义域上的可导函数,“f'(x0)=0”是“y=f(x)在x0处有极值”的充要条件;
③命题“若a>b,则2a>2b﹣1”的否命题为“若a≤b,则2a≤2b﹣1”;
④若“p且q”为假命题,则p、q均为假命题.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥![]() 的底面是边长为3的等边三角形,侧棱
的底面是边长为3的等边三角形,侧棱![]() 设点M,N分别为PC,BC的中点.
设点M,N分别为PC,BC的中点.
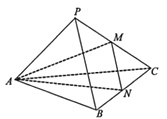
(Ⅰ)求证:BC⊥面AMN;
(Ⅱ)求直线AP与平面AMN所成角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com