利用函数的单调性定义证明函
f(x)=,x∈[2,4]是单调递减函数,并求函数的值域.
证明:在[2,4]上任x
1,x
2.x
1<x
2,f(x
1)=
,f(x
2)=
∴
f(x1)-f(x2)=-=
∵2≤x
1<x
2≤4,∴x
2-x
1>0,x
1-1>0,x
2-1>0
∴f(x
1)-f(x
2)>0,
∴f(x
1)>f(x
2),∴f(x)是在[2,4]上的减函数
当x=2时函数取最大值2,当x=4时函数取最小值
因此,函数的值域
[,2].
练习册系列答案
相关习题
科目:高中数学
来源:
题型:
利用函数的单调性定义证明函
f(x)=,x∈[2,4]是单调递减函数,并求函数的值域.
查看答案和解析>>
科目:高中数学
来源:
题型:
利用函数的单调性定义证明函数f(x)=ax
2+bx+c(a>0)在区间(-∞,-

)上是减函数.
查看答案和解析>>
科目:高中数学
来源:
题型:
利用函数的单调性定义研究函数f(x)=

在定义域内的单调性.
查看答案和解析>>
科目:高中数学
来源:
题型:
若函数f(x)是
R上的增函数,且恒有f(x)>0,设F(x)=

.利用函数的单调性定义证明函数F(x)是
R上的减函数.
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
利用函数的单调性定义证明函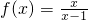 ,x∈[2,4]是单调递减函数,并求函数的值域.
,x∈[2,4]是单调递减函数,并求函数的值域.
查看答案和解析>>
