
【题目】为响应党中央“扶贫攻坚”的号召,某单位指导一贫困村通过种植紫甘薯来提高经济收入.紫甘薯对环境温度要求较高,根据以往的经验,随着温度的升高,其死亡株数成增长的趋势.下表给出了2018年种植的一批试验紫甘薯在不同温度时6组死亡的株数:
温度 | 21 | 23 | 24 | 27 | 29 | 32 |
死亡数 | 6 | 11 | 20 | 27 | 57 | 77 |
经计算:![]() ,
,![]() ,
,![]() ,
,![]() .
.
其中![]() 分别为试验数据中的温度和死亡株数,
分别为试验数据中的温度和死亡株数,![]() .
.
(1)![]() 与
与![]() 是否有较强的线性相关性? 请计算相关系数
是否有较强的线性相关性? 请计算相关系数![]() (精确到
(精确到![]() )说明.
)说明.
(2)并求![]() 关于
关于![]() 的回归方程
的回归方程![]() (
(![]() 和
和![]() 都精确到
都精确到![]() );
);
(3)用(2)中的线性回归模型预测温度为![]() 时该批紫甘薯死亡株数(结果取整数).
时该批紫甘薯死亡株数(结果取整数).
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,
,
①线性相关系数 ,通常情况下当
,通常情况下当![]() 大于0.8时,认为两
大于0.8时,认为两
个变量有很强的线性相关性.
②其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
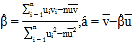 ;
;
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】某单位需要从甲、乙两人中选拔一人参加新岗位培训,特别组织了5个专项的考试,成绩统计如下:
第一项 | 第二项 | 第三项 | 第四项 | 第五项 | |
甲的成绩 | 81 | 82 | 79 | 96 | 87 |
乙的成绩 | 94 | 76 | 80 | 90 | 85 |
(1)根据有关统计知识,回答问题:若从甲、乙2人中选出1人参加新岗位培训,你认为选谁合适,请说明理由;
(2)根据有关概率知识,解答以下问题:
从甲、乙两人的成绩中各随机抽取一个,设抽到甲的成绩为![]() ,抽到乙的成绩为
,抽到乙的成绩为![]() ,用
,用![]() 表示满足条件
表示满足条件![]() 的事件,求事件
的事件,求事件![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年“十一”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(![]() )分成六段:
)分成六段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,后得到如图的频率分布直方图.
,后得到如图的频率分布直方图.
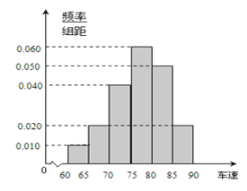
(1)求这40辆小型车辆车速的众数和中位数的估计值;
(2)若从车速在![]() 的车辆中任抽取2辆,求车速在
的车辆中任抽取2辆,求车速在![]() 的车辆恰有一辆的概率.
的车辆恰有一辆的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥P-ABC中,PC![]() 平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD![]() 平面PAB
平面PAB
(1)求证:AB![]() 平面PCB
平面PCB
(2)求异面直线AP与BC所成角的大小
(3)求二面角C-PA-B 的大小的余弦值

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x3-6x2+9x-abc,a<b<c,且f(a)=f(b)=f(c)=0.现给出如下结论:
①f(0)f(1)>0; ②f(0)f(1)<0;
③f(0)f(3)>0; ④f(0)f(3)<0.
其中正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四边形OABP是平行四边形,过点P的直线与射线OA,OB分别相交于点M,N,若 ![]() ,
, ![]() .
. 
(1)把y用x表示出来(即求y=f(x)的解析式);
(2)设数列{an}的首项a1=1,前n项和Sn满足Sn=f(Sn﹣1)(n≥2且n∈N*),求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有甲,乙两个靶,某射手向甲靶射击一次,命中的概率是 ![]() ,向乙靶射击两次,每次命中的概率是
,向乙靶射击两次,每次命中的概率是 ![]() ,若该射手每次射击的结果相互独立,则该射手完成以上三次射击恰好命中一次的概率是( )
,若该射手每次射击的结果相互独立,则该射手完成以上三次射击恰好命中一次的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com