练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某成衣批发店为了对一款成衣进行合理定价，将该款成衣按事先拟定的价格进行试销，得到了如下数据：

    批发单价x（元）

    80

    82

    84

    86

    88

    90

    销售量y（件）

    90

    84

    83

    80

    75

    68


    （1）求回归直线方程 ，其中
    （2）预测批发单价定为85元时，销售量大概是多少件？
    （3）假设在今后的销售中，销售量与批发单价仍然服从（1）中的关系，且该款成衣的成本价为40元/件，为使该成衣批发店在该款成衣上获得更大利润，该款成衣单价大约定为多少元？

    【答案】
    （1）解： =85， =80，

    ∵回归直线方程 ，其中 ，

    ∴a=250，

    ∴y=﹣2x+250


    （2）解：x=85时，y=﹣170+250=80，即销售量大概是80件
    （3）解：设该款成衣单价大约定为x元，则利润L=（x﹣40）（﹣2x+250）= ，

    ∴x=82.5元，该成衣批发店在该款成衣上获得更大利润


    【解析】（1）求出样本中心点，即可求出回归直线方程；（2）x=85时，y=﹣170+250=80，即可得到销售量；（3）设该款成衣单价大约定为x元，则利润L=（x﹣40）（﹣2x+250）= ，即可得出结论．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，定圆C的半径为4，A为圆C上的一个定点，B为圆C上的动点，若点A，B，C不共线，且 对任意的t∈（0，+∞）恒成立，则 = ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】学校为了解学生在课外读物方面的支出情况，抽取了n名同学进行调查，结果显示这些同学的支出都在[10,50)(单位：元)，其中支出在[30,50)(单位：元)的同学有67人，其频率分布直方图如图所示，则n的值为(　　)

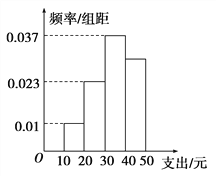
    A. 100 B. 120 C. 130 D. 390

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列满足， ，其中.

    （1）设，求证：数列是等差数列，并求出的通项公式；

    （2）设，数列的前项和为，是否存在正整数，使得对于恒成立，若存在，求出的最小值，若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】点E、F、G分别是正方体ABCD－A1B1C1D1的棱AB、BC、B1C1的中点，如图所示，则下列命题中的真命题是________(写出所有真命题的编号)．

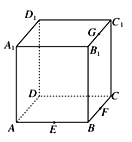
    ①以正方体的顶点为顶点的三棱锥的四个面中最多只有三个面是直角三角形；

    ②过点F、D1、G的截面是正方形；

    ③点P在直线FG上运动时，总有AP⊥DE；

    ④点Q在直线BC1上运动时，三棱锥A－D1QC的体积是定值；

    ⑤点M是正方体的平面A1B1C1D1内的到点D和C1距离相等的点，则点M的轨迹是一条线段．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某书店销售刚刚上市的某知名品牌的高三数学单元卷，按事先拟定的价格进行5天试销，每种单价试销1天，得到如下数据：

    单价（元）

    18

    19

    20

    21

    22

    销量（册）

    61

    56

    50

    48

    45

    （1）求试销5天的销量的方差和对的回归直线方程；

    （2）预计今后的销售中，销量与单价服从（1）中的回归方程，已知每册单元卷的成本是14元，为了获得最大利润，该单元卷的单价卷的单价应定为多少元？

    （附：）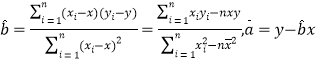

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题10分） 从3名男生和名女生中任选2人参加比赛。

    ①求所选2人都是男生的概率;

    ②求所选2人恰有1名女生的概率;

    ③求所选2人中至少有1名女生的概率

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】近期中央电视台播出的《中国诗词大会》火遍全国，下面是组委会在选拔赛时随机抽取的100名选手的成绩，按成绩分组，得到的频率分布表如下所示：

    组号

    分组

    频数

    频率

    第1组

    第2组

    ①

    第3组

    20

    ②

    第4组

    20

    第5组

    10

    合计

    100

    （1）请先求出频率分布表中①、②位置的相应数据，再完成频率分布直方图（用阴影表示）；

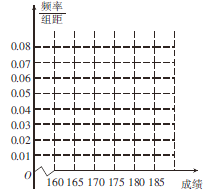
    （2）为了能选拔出最优秀的选手，组委会决定在笔试成绩高的第3、4、5组中用分层抽样抽取5名选手进入第二轮面试，求第3、4、5组每组各抽取多少名选手进入第二轮面试；

    （3）在（2）的前提下，组委会决定在5名选手中随机抽取2名选手接受考官进行面试，求：第4组至少有一名选手被考官面试的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义平面向量之间的一种运算“⊙”如下：对任意的 ，令 ⊙ =mq-np，下面说法错误的是（ ）
    A.若 与 共线，则 ⊙ =0
    B. ⊙ = ⊙
    C.对任意的λ∈R，有 ⊙ = ⊙ ）
    D.（ ⊙ ）2+（ ）2=| |2| |2

    查看答案和解析>>

    同步练习册答案