
 ij���佫10������ƽ���ֳɼס�������ӹ�ij��������ڵ�λʱ����ÿ�������ӹ��ĺϸ����������ʮλ����Ϊ������λ����ΪҶ�õ��ľ�Ҷͼ��ͼ��ʾ����֪�ס����������ݵ�ƽ������Ϊ10��
ij���佫10������ƽ���ֳɼס�������ӹ�ij��������ڵ�λʱ����ÿ�������ӹ��ĺϸ����������ʮλ����Ϊ������λ����ΪҶ�õ��ľ�Ҷͼ��ͼ��ʾ����֪�ס����������ݵ�ƽ������Ϊ10������ ��1�����������ƽ�����ļ��㹫ʽ�ֱ����m��n��ֵ��
��2���ֱ�����ס������鼼���ڵ�λʱ���ڼӹ��ĺϸ�������ķ���${S}_{��}^{2}$��${S}_{��}^{2}$���ٸ������ǵ�ƽ��ֵ��ȣ��ɵ÷����С�ķ��Ӹ��ȶ�һЩ��
��3�����оٷ�������еĻ����¼��ĸ������ҳ���������ó��䡰�����ϸĻ����¼��ĸ�����������øó��䡰�����ϸĸ��ʣ�
��� �⣺��1���������$\overline{x_��}=\frac{1}{5}��{7+8+10+12+10+m}��=10$��
���m=3��
����$\overline{x_��}=\frac{1}{5}��{n+9+10+11+12}��=10$��
���n=8��
��2���ֱ�����ס������鼼���ڵ�λʱ���ڼӹ��ĺϸ�������ķ��
$S_��^2=\frac{1}{5}[{{{��{7-10}��}^2}+{{��{8-10}��}^2}+{{��{10-10}��}^2}+{{��{12-10}��}^2}+{{��{13-10}��}^2}}]=5.2$��
$S_��^2=\frac{1}{5}[{{{��{8-10}��}^2}+{{��{9-10}��}^2}+{{��{10-10}��}^2}+{{��{11-10}��}^2}+{{��{12-10}��}^2}}]=2$��
����$\overline{x_��}=\overline{x_��}��S_��^2��S_��^2$��
�ɵ����鼼��ˮƽ�����൱��������ȶ�Щ��
��3���ʼ첿�ŴӸó���ס������鼼���и������ȡһ��������
����ӹ���������м�飬�����˼ӹ��ĺϸ�������ֱ�Ϊ��a��b����
�����еģ�a��b���У�
��7��8������7��9������7��10������7��11������7��12����
��8��8������8��9������8��10������8��11������8��12����
��10��8������10��9������10��10������10��11������10��12����
��12��8������12��9������12��10������12��11������12��12����
��13��8������13��9������13��10������13��11������13��12��������25����
������a+b��17�Ļ����¼��У�
��7��8������7��9������7��10������8��8������8��9��������5�������¼���
������a+b��17�Ļ����¼�����Ϊ25-5=20��
���Ըó��䡰�����ϸĸ���Ϊ$\frac{20}{25}=\frac{4}{5}$��
���� ������Ҫ���鷽��Ķ�������ŵ�������⣬�����оٳ����鷢���������¼��������������¼����оٷ����ǽ���ŵ���������һ����Ҫ�Ľ��ⷽ���������е���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�� | B�� | �� | C�� | $\frac{��}{2}$-�� | D�� | $\frac{3��}{2}$-�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ƽ���ı��� | B�� | ���� | C�� | �������� | D�� | ���������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
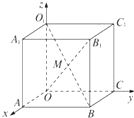 ��ͼ��ʾ���ڳ�����OABC-O1A1B1C1�У�|OA|=2��|AB|=3��|AA1|=3��M��OB1��BO1�Ľ��㣬��M���������$��1��\frac{3}{2}��\frac{3}{2}��$��
��ͼ��ʾ���ڳ�����OABC-O1A1B1C1�У�|OA|=2��|AB|=3��|AA1|=3��M��OB1��BO1�Ľ��㣬��M���������$��1��\frac{3}{2}��\frac{3}{2}��$���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com