
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 (1),∵f′(x)=3ax2+2bx+c(a≠0),若f(x)存在极值,则△>0,则一定既有极大值又有极小值;
(2),若椭圆$\frac{x^2}{4}+\frac{y^2}{m}$=1离心率为$\frac{1}{2}$”,则当m>4时,$\frac{m-4}{m}=\frac{1}{4}$⇒m=$\frac{16}{3}$;
(3),设z∈C,z=a+bi(a、b为实数)“若z=$\overline{z}$“,则a+bi=a-bi⇒b=0,⇒z为实数;
(4),若b=0,复数z=a+bi为实数;
解答 解:对于(1),∵f′(x)=3ax2+2bx+c(a≠0),若f(x)存在极值,则△>0,则一定既有极大值又有极小值,故正确;
对于(2),若椭圆$\frac{x^2}{4}+\frac{y^2}{m}$=1离心率为$\frac{1}{2}$”,则当m>4时,$\frac{m-4}{m}=\frac{1}{4}$⇒m=$\frac{16}{3}$,故错;
对于(3),设z∈C,z=a+bi(a、b为实数)“若z=$\overline{z}$“,则a+bi=a-bi⇒b=0,⇒z为实数,故正确;
对于(4),若b=0,复数z=a+bi为实数,故错;
故选:B.
点评 本题考查了命题真假的判定,属于基础题.


 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x1)<f(x2) | B. | f(x1)=f(x2) | ||
| C. | f(x1)>f(x2) | D. | f(x1)、f(x&2)的大小不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ①② | C. | ①②③④ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
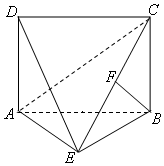 如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.
如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com