练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在棱长为6的正方体ABCD﹣A1B1C1D1中，M是BC的中点，点P是面DCC1D1内的动点，且满足∠APD=∠MPC，则三棱锥P﹣BCD的体积最大值是（ ）
    A.36
    B.12
    C.24
    D.18

    【答案】B
    【解析】解：∵在棱长为6的正方体ABCD﹣A1B1C1D1中，M是BC的中点，点P是面DCC1D1所在的平面内的动点，且满足∠APD=∠MPC， ∴Rt△ADP∽△Rt△PMC，
    ∴ = =2，
    即PD=2PC，
    设DO=x，PO=h，作PO⊥CD，
    ∴ ，化简得：3h2=﹣3x2+48x﹣144，0≤x≤6，
    根据函数单调性判断：x=6时，3h2最大值为36，
    h大=2 ，
    ∵在正方体中PO⊥面BCD，
    ∴三棱锥P﹣BCD的体积最大值： =12 ，
    故选：B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）是定义在R上的函数，满足f（x）=f（4﹣x），且对任意x1 ， x2∈（0，+∞），都有（x1﹣x2）[f（x1+2）﹣f（x2+2）]＞0，则满足f（2﹣x）=f（ ）的所有x的和为（ ）
    A.﹣3
    B.﹣5
    C.﹣8
    D.8

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中， 平面.

    （1）求证： 平面；

    （2）若为线段的中点，且过三点平面与线段交于点，确定的位置，说明理由；

    并求三棱锥的高.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知实数x，y满足方程（x﹣2）2+（y﹣2）2=1．
    （1）求 的取值范围；
    （2）求|x+y+l|的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ，且该函数的图象过点（1，5）． （Ⅰ）求f（x）的解析式，并判断f（x）的奇偶性；
    （Ⅱ）判断f（x）在区间（0，2）上的单调性，并用函数单调性的定义证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列方程表示的直线倾斜角为135°的是（ ）
    A.y=x﹣1
    B.y﹣1= （x+2）
    C. + =1
    D. x+2y=0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，多面体OABCD，AB=CD=2，AD=BC= ，AC=BD= ，且OA，OB，OC两两垂直，则下列说法正确的是（ ）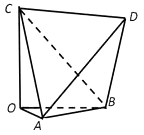
    A.直线OB∥平面ACD
    B.球面经过点A，B，C，D四点的球的直径是
    C.直线AD与OB所成角是45°
    D.二面角A﹣OC﹣D等于30°

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=Asin（ωx+）（A＞0，ω＞0，||＜π）图象的最高点D的坐标为 ，与点D相邻的最低点坐标为 ． （Ⅰ）求函数f（x）的解析式；
    （Ⅱ）求满足f（x）=1的实数x的集合．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥P﹣ABCD中，PD⊥底面ABCD，AB∥DC，AD⊥DC，AB=AD=1，DC=2，PD ，M为棱PB的中点． （Ⅰ）证明：DM⊥平面PBC；
    （Ⅱ）求二面角A﹣DM﹣C的余弦值．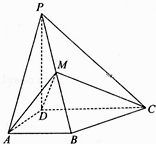

    查看答案和解析>>

    同步练习册答案