
【题目】(1)6个人按下列要求站一横排,甲、乙必须相邻,有多少种不同的站法?
(2)6个人按下列要求站一横排,甲不站左端,乙不站右端.有多少种不同的站法?
(3)用0,1,2,3,4,5这六个数字可以组成多少个六位数且是奇数(无重复数字的数)?
(4)用0,1,2,3,4,5这六个数字可以组成多少个个位上的数字不是5的六位数(无重复数字的数)?
【答案】(1)240;(2)504;(3)288;(4)504.
【解析】
(1)相邻问题采用“捆绑法”,即可得出结果;
(2)采用特殊位置优先法,先考虑有限制条件的位置的要求,再考虑其他位置,即可得解;
(3)先求出个位数的排列数,然后对首位数进行考虑,注意首位不能为0,再对剩余位进行排列,最后将排列数相乘即可得出结果;
(4)当个位为0时,剩余可随意排列,当个位不为0时,先对个位进行排列,在考虑首位不为零的问题,剩余位随意排列,然后将两种情况相加即可得出结果.
(1)把甲乙看成一个整体后,进行全排列,有![]() 种排法,
种排法,
再对甲乙进行全排列,有![]() 种排法,
种排法,
所以共有![]() 种排法;
种排法;
(2)当甲在右端时,其余的5个人任意排,有![]() 种排法,
种排法,
当甲不在右端时,因为甲不在左端,所以甲有4种排法,
再排乙,乙有4种排法,最后,其余人任意排,有![]() 种排法,
种排法,
所以,甲不在右端时,共有![]() 种排法,
种排法,
故甲不站左端,乙不站右端的排法有![]() 种;
种;
(3)第一步,排个位,有![]() 种排法;
种排法;
第二步,排十万位,有![]() 种排法;
种排法;
第三步,排其他位,有![]() 种排法,
种排法,
根据分步乘法计数原理,共有![]() 个六位奇数,
个六位奇数,
用![]() 这六个数字可以组成
这六个数字可以组成![]() 个六位数且是奇数;
个六位数且是奇数;
(4)当个位为0时,有![]() 种排法;
种排法;
当个位不为0时,有![]() 种排法;
种排法;
![]() ,
,
所以,用![]() 这六个数字可以组成
这六个数字可以组成![]() 个个位上的数字不是5的六位数.
个个位上的数字不是5的六位数.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】2018年是中国改革开放的第40周年,为了充分认识新形势下改革开放的时代性,某地的民调机构随机选取了该地的100名市民进行调查,将他们的年龄分成6段:![]() ,并绘制了如图所示的频率分布直方图.
,并绘制了如图所示的频率分布直方图.

(1)现从年龄在![]() 内的人员中按分层抽样的方法抽取8人,再从这8人中随机抽取3人进行座谈,用
内的人员中按分层抽样的方法抽取8人,再从这8人中随机抽取3人进行座谈,用![]() 表示年龄在
表示年龄在![]() 内的人数,求
内的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若用样本的频率代替概率,用随机抽样的方法从该地抽取20名市民进行调查,其中有![]() 名市民的年龄在
名市民的年龄在![]() 的概率为
的概率为![]() .当
.当![]() 最大时,求
最大时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解本市的交通状况,某校高一年级的同学分成了甲、乙、丙三个组,从下午13点到18点,分别对三个路口的机动车通行情况进行了实际调查,并绘制了频率分布直方图(如图),记甲、乙、丙三个组所调查数据的标准差分别为![]() ,则它们的大小关系为( )
,则它们的大小关系为( )

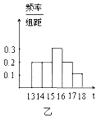
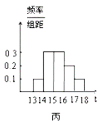
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】回答下列两个问题, 并给出例子或证明.
(1)对任意正整数![]() , 在平面上是否都存在
, 在平面上是否都存在![]() 个不在同一条直线上的点, 使得任意两点间的距离都为正整数?
个不在同一条直线上的点, 使得任意两点间的距离都为正整数?
(2)在平面上是否存在两两不同的无限点列组成的点集![]() , 使得
, 使得![]() 内所有点不在同一条直线上, 且
内所有点不在同一条直线上, 且![]() 内任意两点间的距离为正整数?
内任意两点间的距离为正整数?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,当
上的偶函数,当![]() 时,
时,![]() .现已画出函数
.现已画出函数![]() 在
在![]() 轴右侧的图象,如图所示.
轴右侧的图象,如图所示.
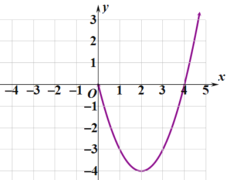
(1)画出函数![]() 在
在![]() 轴左侧的图象,根据图象写出函数
轴左侧的图象,根据图象写出函数![]() 在
在![]() 上的单调区间;
上的单调区间;
(2)求函数![]() 在
在![]() 上的解析式;
上的解析式;
(3)解不等式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知对任意平面向量![]() ,把
,把![]() 绕其起点沿逆时针方向旋转
绕其起点沿逆时针方向旋转![]() 角得到向量
角得到向量![]() ,叫做把点
,叫做把点![]() 绕点
绕点![]() 逆时针方向旋转
逆时针方向旋转![]() 角得到点
角得到点![]() .
.
(1)已知平面内点![]() ,点
,点![]() .把点
.把点![]() 绕点
绕点![]() 沿顺时针方向旋转
沿顺时针方向旋转![]() 后得到点
后得到点![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)设平面内曲线![]() 上的每一点绕坐标原点沿逆时针方向旋转
上的每一点绕坐标原点沿逆时针方向旋转![]() 后得到的点的轨迹是曲线
后得到的点的轨迹是曲线![]() ,求原来曲线
,求原来曲线![]() 的方程,并求曲线
的方程,并求曲线![]() 上的点到原点距离的最小值.
上的点到原点距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com