
【题目】已知函数f(x)=2x+1,数列{an}满足an=f(n)(n∈N*),数列{bn}的前n项和为Tn , 且b1=2,Tn=bn+1﹣2(n∈N).
(1)分别求{an},{bn}的通项公式;
(2)定义x=[x]+(x),[x]为实数x的整数部分,(x)为小数部分,且0≤(x)<1.记cn= ![]() ,求数列{cn}的前n项和Sn .
,求数列{cn}的前n项和Sn .
【答案】
(1)解:an=f(n)=2n+1.
当n≥2时,bn=Tn﹣Tn﹣1=bn+1﹣bn,bn+1=2bn,b1=2≠0,又令n=1,得b2=4.
∴ ![]() ,{bn}是以2为首项和公比的等比数列,
,{bn}是以2为首项和公比的等比数列,
![]() .
.
(2)解:依题意, ![]() ;
; ![]() ;
;
当n≥3时,可以证明0<2n+1<2n,即 ![]() ,∴
,∴ ![]() ,
,
则 ![]() ,
, ![]() ,
, ![]() .
.
令 ![]() ,
, ![]() ,
,
两式相减并化简得得 ![]() .
.
∴ ![]() ,检验知,n=1不合,n=2适合,
,检验知,n=1不合,n=2适合,
∴ 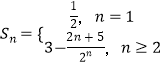
【解析】(1)an=f(n)=2n+1.当n≥2时,bn=Tn﹣Tn﹣1 , 可得bn+1=2bn , b1=2≠0,又令n=1,得b2=4,利用等比数列的通项公式即可得出.(2)由题意, ![]() ;
; ![]() ;当n≥3时,可以证明0<2n+1<2n , 因此
;当n≥3时,可以证明0<2n+1<2n , 因此 ![]() ,再利用“错位相减法”与等比数列的前n项和公式即可得出.
,再利用“错位相减法”与等比数列的前n项和公式即可得出.
【考点精析】掌握数列的前n项和和数列的通项公式是解答本题的根本,需要知道数列{an}的前n项和sn与通项an的关系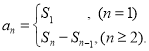 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


 精英口算卡系列答案
精英口算卡系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣1|+|x+3|.
(1)解不等式f(x)≥8;
(2)若不等式f(x)<a2﹣3a的解集不是空集,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在以A,B,C,D,E,F为顶点的多面体中,AF⊥平面ABCD,DE⊥平面ABCD,AD∥BC,AB=CD,∠ABC=60°,BC=AF=2AD=4DE=4. 
(Ⅰ)请在图中作出平面α,使得DEα,且BF∥α,并说明理由;
(Ⅱ)求直线EF与平面BCE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数 ![]() 的图象如图所示,为了得到g(x)=cos2x的图象,则只需将f(x)的图象( )
的图象如图所示,为了得到g(x)=cos2x的图象,则只需将f(x)的图象( ) 
A.向右平移 ![]() 个单位长度
个单位长度
B.向右平移 ![]() 个单位长度
个单位长度
C.向左平移 ![]() 个单位长度
个单位长度
D.向左平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 为常数).
为常数).
(1)判断函数![]() 的奇偶性;
的奇偶性;
(2)若不等式![]() 在
在![]() 时有解,求实数
时有解,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,是否存在正数
,是否存在正数![]() ,使得对于区间
,使得对于区间![]() 上的任意三个实数
上的任意三个实数![]() ,
,![]() ,
,![]() ,都存在以
,都存在以![]() ,
,![]() ,
,![]() 为边长的三角形?若存在,试求出这样的
为边长的三角形?若存在,试求出这样的![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,AD∥BC,BC⊥CD,点P在底面ABCD上的射影为A,BC=CD= ![]() AD=1,E为棱AD的中点,M为棱PA的中点.
AD=1,E为棱AD的中点,M为棱PA的中点. 
(1)求证:BM∥平面PCD;
(2)若∠ADP=45°,求二面角A﹣PC﹣E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别是角A,B,C的对边,a,b,c成等比数列,且a2﹣c2=ac﹣bc.
(Ⅰ)求∠A的大小;
(Ⅱ)若a= ![]() ,且sinA+sin(B﹣C)=2sin2C,求△ABC的面积.
,且sinA+sin(B﹣C)=2sin2C,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在![]() 上的函数
上的函数![]() 满足条件:存在实数
满足条件:存在实数![]() 且
且![]()
![]() ,使得:
,使得:
⑴ 任取![]() ,有
,有![]() (
(![]() 是常数);
是常数);
⑵ 对于![]() 内任意
内任意![]() ,当
,当![]() ,总有
,总有![]() .
.
我们将满足上述两条件的函数![]() 称为“平顶型”函数,称
称为“平顶型”函数,称![]() 为“平顶高度”,称
为“平顶高度”,称![]() 为“平顶宽度”.根据上述定义,解决下列问题:
为“平顶宽度”.根据上述定义,解决下列问题:
(1)函数![]() 是否为“平顶型”函数?若是,求出“平顶高度”和“平顶宽度”;若不是,简要说明理由.
是否为“平顶型”函数?若是,求出“平顶高度”和“平顶宽度”;若不是,简要说明理由.
(2) 已知![]() 是“平顶型”函数,求出
是“平顶型”函数,求出![]() 的值.
的值.
(3)对于(2)中的函数![]() ,若
,若![]() 在
在![]() 上有两个不相等的根,求实数
上有两个不相等的根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com