
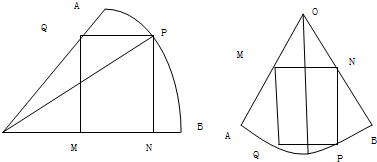
分析 将图二可拆分成两个图一的形式,可以类比得到结论.图一角是2α,图二拆分后角是α,故矩形面积的最大值为$\frac{1}{2}$r2tan$\frac{α}{2}$,由此可得结论.
解答  解:图一,设半径为2的扇形AOB圆心角为2α=$\frac{π}{3}$,∠MOQ=x,则MQ=rsinx,
解:图一,设半径为2的扇形AOB圆心角为2α=$\frac{π}{3}$,∠MOQ=x,则MQ=rsinx,
在△OMN中,$\frac{MN}{sin(2α-x)}=\frac{r}{sin(180°-2α)}$,
∴MN=$\frac{rsin(2α-x)}{sin2α}$,
∴矩形面积S=$\frac{{r}^{2}sin(2α-x)sinx}{sin2α}$=$\frac{{r}^{2}}{2sin2α}$[cos(2x-2α)-cos2α]≤$\frac{{r}^{2}}{2sin2α}$[1-cos2α]=$\frac{1}{2}$r2tanα,
当且仅当x=α时,取得最大值,故图一矩形面积的最大值为$\frac{1}{2}$r2tanα=$\frac{1}{2}×{2}^{2}×tan30°$=$\frac{2\sqrt{3}}{3}$,
图二可拆分成两个,图一角是2α,图二拆分后角是α,故根据图1得出的结论,可得矩形面积的最大值为$\frac{1}{2}$r2tan$\frac{α}{2}$,
而图二时由两个这样的图形组成,所以两个则为r2tan$\frac{α}{2}$.
故答案为:r2tan$\frac{α}{2}$=22×tan$\frac{π}{12}$=4(2-$\sqrt{3}$),
显然$\frac{2\sqrt{3}}{3}$>4(2-$\sqrt{3}$),
所以内接矩形的最大面积为$\frac{2\sqrt{3}}{3}$.
点评 本题考查扇形内接矩形面积问题,考查学生分析解决问题的能力,解题的关键是发现两个图之间的联系,利用已有的结论进行解题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | d<0且a1>0 | B. | d>0且a1>0 | C. | d<0且a2>0 | D. | d>0且a2>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com