已知函数f(x)=x3+ax2+bx+1的图象过M(1,5),且在M处的切线的斜率为8.
(1)求a、b的值;
(2)求函数f(x)的单调区间;
(3)求f(x)在[-1,1]上的最值.
解:(1)f'(x)=3x
2+2ax+b由已知
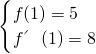
∴
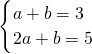
∴

(2)f'(x)=3x
2+4x+1=(3x+1)(x+1)
由f'(x)>0得
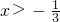
或x<-1
由f'(x)<0得
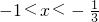
∴f(x)的单调增区间为
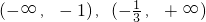
,单调减区间为
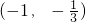
;
(3)∴由(2)知在

上是减函数,在
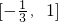
上是增函数
∴f(x)在[-1,1]上的最小值为
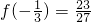
,
又f(-1)=1,f(1)=5
∴f(x)在[-1,1]上的最大值为5
综合得:f(x)在[-1,1]上的最小值为

,最大值为:5
分析:(1)求出f′(x),因为函数在M处切线的斜率为8,则f′(1)等于8,把(1,5)代入f(x)得到f(1)=5,联立即可求出a与b的值;(2)把(1)求出的a与b的值代入到f′(x)后,令f′(x)大于0解出x的范围即为函数的增区间,令f′(x)小于0解出x的范围即为函数的减区间;(3)在闭区间[-1,1]上,由(2)知在

上是减函数,在
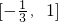
上是增函数,即可得到函数的最小值为f(-

),然后分别求出f(-1)和f(1)比较大小得到函数的最大值即可.
点评:此题考查学生会求曲线上过某点切线的斜率,会利用导函数的正负研究原函数的增减性,会利用导数求闭区间上函数的最值,是一道中档题.

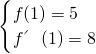 ∴
∴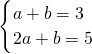 ∴
∴
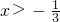 或x<-1
或x<-1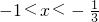
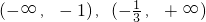 ,单调减区间为
,单调减区间为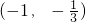 ;
; 上是减函数,在
上是减函数,在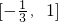 上是增函数
上是增函数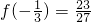 ,
, ,最大值为:5
,最大值为:5 上是减函数,在
上是减函数,在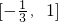 上是增函数,即可得到函数的最小值为f(-
上是增函数,即可得到函数的最小值为f(- ),然后分别求出f(-1)和f(1)比较大小得到函数的最大值即可.
),然后分别求出f(-1)和f(1)比较大小得到函数的最大值即可.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<