
【题目】已知 ![]() ,且方程
,且方程 ![]() 无实数根,下列命题:
无实数根,下列命题:
(1)方程 ![]() 一定有实数根;
一定有实数根;
(2)若 ![]() ,则不等式
,则不等式 ![]() 对一切实数
对一切实数 ![]() 都成立;
都成立;
(3)若 ![]() ,则必存在实数
,则必存在实数 ![]() ,使
,使 ![]() ;
;
(4)若 ![]() ,则不等式
,则不等式 ![]() 对一切实数
对一切实数 ![]() 都成立.
都成立.
其中,正确命题的序号是________________.(把你认为正确的命题的所有序号都填上)
【答案】(2)(4)
【解析】∵由函数f(x)=ax2+bx+c(a≠0),且方程f(x)=x无实数根,
即y=ax2+bx+c与y=x的图象无交点,
∴(1)函数y=f[f(x)]与y=x的图象无交点,即方程f[f(x)]=x没有实数根,(1)错误;
(2)当a>0时,函数f(x)=ax2+bx+c(a≠0)的图象开口向上,与y=x无交点,
∴f(x)的图象在y=x图象的上方,
∴不等式f[f(x)]>x对一切实数x都成立,(2)正确;
(3)同理,当a<0时,函数f(x)=ax2+bx+c(a≠0)的图象在y=x的下方,
f[f(x)]<x恒成立,∴(3)错误;
(4)当a+b+c=0时,f(1)=0,结合题意知a<0,函数f(x)=ax2+bx+c(a≠0)的图象在y=x的下方,
不等式f[f(x)]<x对一切x都成立,∴(4)正确.
综上,正确的答案为(2)(4).
故答案为(2)(4)


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某教研机构随机抽取某校20个班级,调查各班关注汉字听写大赛的学生人数,根据所得数据的茎叶图,以组距为5将数据分组成![]() 时,所作的频率分布直方图如图所示,则原始茎叶图可能是( )
时,所作的频率分布直方图如图所示,则原始茎叶图可能是( )
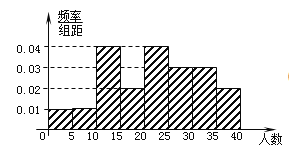
A.  B.
B. 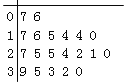
C. 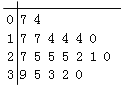 D.
D. 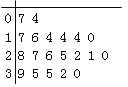
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 满足
满足 ![]() (其中
(其中 ![]() ,
, ![]() ).
).
(1)求 ![]() 的表达式;
的表达式;
(2)对于函数 ![]() ,当
,当 ![]() 时,
时, ![]() ,求实数
,求实数 ![]() 的取值范围.
的取值范围.
(3)当 ![]() 时,
时, ![]() 的值为负数,求
的值为负数,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,右焦点
,右焦点![]() ,过点
,过点 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,求证:
,求证: ![]() 三点共线;
三点共线;
(3) 当![]() 面积最大时,求直线
面积最大时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年入冬以来,各地雾霾天气频发, ![]() 频频爆表(
频频爆表(![]() 是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与
是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与![]() 的浓度是否相关,某市现采集周一到周五某一时间段车流量与
的浓度是否相关,某市现采集周一到周五某一时间段车流量与![]() 的数据如下表:
的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量 | 50 | 51 | 54 | 57 | 58 |
| 69 | 70 | 74 | 78 | 79 |
(1)请根据上述数据,在下面给出的坐标系中画出散点图;
(2)试判断![]() 与
与![]() 是否具有线性关系,若有请求出
是否具有线性关系,若有请求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,若没有,请说明理由;
,若没有,请说明理由;
(3)若周六同一时间段的车流量为60万辆,试根据(2)得出的结论,预报该时间段的![]() 的浓度(保留整数).
的浓度(保留整数).
参考公式: 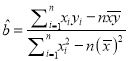
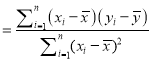 ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com