已知f(x)=lnx-x2+bx+3.
(Ⅰ)若函数f(x)在点(2,y)处的切线与直线2x+y+2=0垂直,求函数f(x)在区间[1,3]上的最小值;
(Ⅱ)若f(x)在区间[1,m]上单调,求b的取值范围.
分析:(Ⅰ)首先求出函数的导数f′(x),令x=2求出函数f(x)在点(2,y)的斜率,然后根据函数f(x)在点(2,y)处的切线与直线2x+y+2=0垂直,求出函数f(x)的表达式,根据导数判断函数的单调性,从而求函数f(x)在区间[1,3]上的最小值;
(Ⅱ)由(Ⅰ)求出函数的单调区间,可知y=2x-
在[1,m]上单调递增,在[1,m]上恒成立,从而求出b的取值范围.
解答:解:(1)
f′(x)=-2x+b直线2x+y+2=0斜率为-2,
令f′(2)=
得b=4,∴f(x)=lnx-x
2+4x+3
∴
f′(x)=-2x+4==0得x=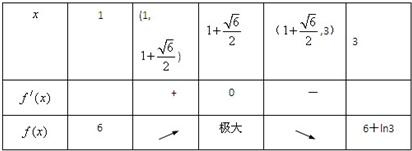
∵6+ln3>6,∴x=1时,f(x)在[1,3]上最小值6;(6分)
(2)令
f′(x)=-2x+b≥0得b≥2x-
,
在[1,m]上恒成立而y=2x-
在[1,m]上单调递增,
最大值为2m-
,∴b≥2m-
令
f′(x)=-2x+b≤0得b≤2x-
,
在[1,m]上恒成立而y=2x-
在[1,m]单调递增,最小值为y=1,
∴b≤1
故b≥2m-
或b≤1时f(x)在[1,m]上单调. (12分)
点评:此题主要考查函数导数与函数单调性之间的关系,需要掌握并会熟练运用导数判断函数的单调性.



