
【题目】已知定义域为![]() 的奇函数
的奇函数![]() ,当
,当![]() 时,满足
时,满足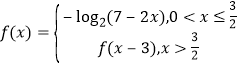 ,
,
则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】分析:通过计算前几项,可得n=3,4,…,2018,数列以3为周期的数列,计算可得所求和.
详解:定义域为R的奇函数f(x),可得f(﹣x)=﹣f(x),
当x>0时,满足 ,
,
可得x>![]() 时,f(x)=f(x﹣3),
时,f(x)=f(x﹣3),
则f(1)=﹣log25,
f(2)=f(﹣1)=﹣f(1)=log25,
f(3)=f(0)=0,
f(4)=f(1)=﹣log25,
f(5)=f(2)=f(﹣1)=﹣f(1)=log25,
f(6)=f(3)=f(0)=0,
f(7)=f(4)=f(1)=﹣log25,
f(8)=f(2)=f(﹣1)=﹣f(1)=log25,
…
f(1)+f(2)+f(3)+…+f(2020)
=﹣log25+log25+(0﹣log25+log25)×672 =0,
故选:D.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,M(﹣2,0).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,A(ρ,θ)为曲线C上一点,B(ρ,θ+ ![]() ),且|BM|=1.
),且|BM|=1.
(Ⅰ)求曲线C的直角坐标方程;
(Ⅱ)求|OA|2+|MA|2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A、B、C为⊙O上三点,B为 ![]() 的中点,P为AC延长线上一点,PQ与⊙O相切于点Q,BQ与AC相交于点D.
的中点,P为AC延长线上一点,PQ与⊙O相切于点Q,BQ与AC相交于点D.
(Ⅰ)证明:△DPQ为等腰三角形;
(Ⅱ)若PC=1,AD=PD,求BDQD的值.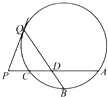
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 (t为参数)曲线C的参数方程为
(t为参数)曲线C的参数方程为![]() ,
,![]() 为参数
为参数![]() ,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为
,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为![]()
(![]() Ⅰ)求直线l以及曲线C的极坐标方程;
Ⅰ)求直线l以及曲线C的极坐标方程;
(Ⅱ)设直线l与曲线C交于A、B两点,求三角形PAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】扇形AOB中心角为![]() ,所在圆半径为
,所在圆半径为![]() ,它按如图(Ⅰ)(Ⅱ)两种方式有内接矩形CDEF.
,它按如图(Ⅰ)(Ⅱ)两种方式有内接矩形CDEF.

(1)矩形CDEF的顶点C、D在扇形的半径OB上,顶点E在圆弧AB上,顶点F在半径OA上,设![]() ;
;
(2)点M是圆弧AB的中点,矩形CDEF的顶点D、E在圆弧AB上,且关于直线OM对称,顶点C、F分别在半径OB、OA上,设![]() ;
;
试研究(1)(2)两种方式下矩形面积的最大值,并说明两种方式下哪一种矩形面积最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com