Question

从正方体的八个顶点中任意选择4个顶点，它们可能是如下几种几何体（或平面图形）的4个顶点，这些几何体（或平面图形）是________（写出所有正确的结论的编号）
①矩形；
②不是矩形的平行四边形；
③有三个面为等腰直角三角形，有一个面为等边三角形的四面体；
④每个面都是等边三角形的四面体．

Answer 1

①③④
分析：画出正方体的图形，找出符合①③④条件的图形．利用线线关系判断②的正误，即可．
解答：①正方体的六个面或对角面都是矩形，所以①正确；
②不是矩形的平行四边形，因为正方体的棱与棱的关系只有两种：平行、垂直，所以满足②的图形不存在，②是错误的；
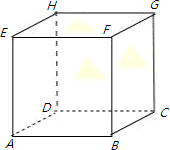
③例如：E-ABD四面体，有三个面为等腰直角三角形，有一个面为等边三角形的四面体；
④例如：E-BDG四面体，每个面都是等边三角形的四面体．
故答案为：①③④．
点评：本题是基础题，考查正方体的结构特征，正方体内的四面体的形状，考查空间想象能力，逻辑推理能力，判断能力．