若中心在原点的双曲线的一条渐近线经过点.则此双曲线的离心率为$\frac{5}{4}$或$\frac{5}{3}$．题目和参考答案——青夏教育精英家教网—

11．若中心在原点的双曲线的一条渐近线经过点（3，-4），则此双曲线的离心率为$\frac{5}{4}$或$\frac{5}{3}$．

分析根据中心在原点的双曲线的一条渐近线经过点（3，-4），$\frac{b}{a}$=$\frac{3}{4}$或$\frac{4}{3}$，利用离心率公式，可得结论．

解答解：∵中心在原点的双曲线的一条渐近线经过点（3，-4），
∴$\frac{b}{a}$=$\frac{3}{4}$或$\frac{4}{3}$，
∴e=$\frac{c}{a}$=$\frac{5}{4}$或$\frac{5}{3}$．
故答案为：$\frac{5}{4}$或$\frac{5}{3}$．

点评本题考查双曲线的简单性质，考查学生的计算能力，比较基础．

练习册系列答案

全景文化中考试题汇编3年真题2年模拟系列答案

金牌教练赢在燕赵系列答案

0系列答案

金题金卷热点测试系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

1．在数列{a_n}，{b_n}中，{a_n}的前n项和为S_n，点（n，S_n）在函数y=x²+2x的图象上．{b_n}满足$\frac{{b}_{n+1}}{{b}_{n}}$=2，b₁=2
（1）求{a_n}，{b_n}的通项公式；
（2）令C_n=a_n•b_n，求数列C_n的前n项和T_n．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

2．

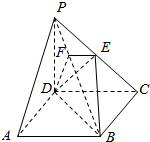如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC=1，点E是PC的中点，作EF⊥PB交PB于点F．
（1）求证：PA∥平面EDB；
（2）求证：PB⊥平面EFD；
（3）在线段AB上是否存在点M，使PM与平面PDB所成角的正弦值为$\frac{{\sqrt{38}}}{19}$？若存在，求出AM的长；若不存在，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

19．

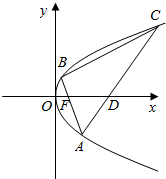已知抛物线T：y²=2px（p＞0）的焦点为F，A（x₀，y₀）为T上异于原点的任意一点，点D为x的正半轴上的点，且有|FA|=|FD|，若x₀=3时，D的横坐标为5．
（1）求T的方程；
（2）直线AF交T于另一点B，直线AD交T于另一点C，试求△ABC的面积S关于x₀的函数关系式S=f（x₀），并求其最小值．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

6．求证：$\frac{1}{n+1}$+$\frac{1}{n+2}$+$\frac{1}{n+3}$+…+$\frac{1}{3n+1}$＜$\frac{9}{8}$．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

16．下列各组函数中，表示同一函数的是（　　）

	A．	$y=x+1与y=\frac{{{x^2}+x}}{x}$		B．	$f（x）=\frac{x^2}{{{{（{\sqrt{x}}）}^2}}}与g（x）=x$
	C．	$f（x）=x\frac{\|x\|}{x}与f（t）=\left\{\begin{array}{l}t（t＞0）\\-t（t＜0）\end{array}\right.$		D．	$f（x）=\|x\|与g（x）=\left\{\begin{array}{l}x（x＞0）\\-x（x＜0）\end{array}\right.$

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

3．已知函数f（x）=|x-1|+|x-a|．
（1）当a=2时，解不等式f（x）≥4；
（2）若不等式f（x）≥a恒成立，求实数a的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

20．将函数f（x）=sin2x的图象向左平移$\frac{π}{4}$个长度单位，得到函数g（x）的图象，则g（x）的单调递增区间是（　　）

A．

（kπ-$\frac{π}{2}$，kπ）（k∈Z）

B．

（kπ，kπ+$\frac{π}{2}$）（k∈Z）

C．

（kπ-$\frac{π}{4}$，kπ+$\frac{π}{4}$）（k∈Z）