练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．若集合A={x|-1≤2x+1≤3}，B=$\{x|\frac{x-2}{x}≤0\}$，则A∪B={x|-1≤x≤2}．

    分析 化简集合A，B，再由并集的含义可得．

    解答 解：集合A={x|-1≤2x+1≤3}={x|-1≤x≤1}，
    B=$\{x|\frac{x-2}{x}≤0\}$={x|0＜x≤2}，
    则A∪B={x|-1≤x≤2}．
    故答案为：{x|-1≤x≤2}．

    点评 本题考查集合的补集运算，同时考查分式不等式的解法，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

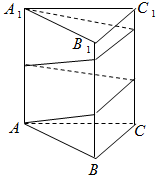    12．已知正三棱柱ABC-A1B1C1的底面边长为4cm，高为10cm，则一质点自点A出发，沿着三棱柱的侧面，绕行两周到达点A1的最短路线的长为（　　）
    A．16cmB．12$\sqrt{3}$cmC．24$\sqrt{3}$cmD．26cm

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．设f（x）为定义在R上的奇函数，其图象关于x=1对称，且f（1）=1，则f（-1）+f（8）=（　　）
    A．-2B．-1C．0D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知等比数列{an}的前6项和S6=21，且4a1、$\frac{3}{2}$a2、a2成等差数列，则an=$\frac{{{2^{n-1}}}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

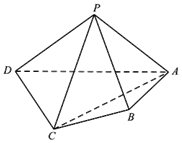    17．如图，在四棱锥P-ABCD中，平面PAD⊥平面ABCD，PA⊥PD，PA=PD，AB⊥AD，AB=1，AD=2，AC=CD=$\sqrt{5}$．
    （1）求证：PD⊥平面PAB；
    （2）求二面角P-CD-A的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．在等差数列{an}中，已知a5=10，a12=31，则公差d=3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

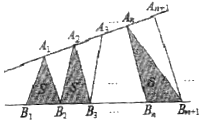    14．如图，点列{An}，{Bn}分别在某个锐角的两边上，且|AnAn+1|=|An+1An+2|，An≠An+2，n∈N*，|BnBn+1|=|Bn+1Bn+2|，Bn≠Bn+2，n∈N*（P≠Q表示P与Q不重合）．若dn=|AnBn|，Sn为△AnBnBn+1的面积，则（　　）
    A．{dn}是等差数列B．{dn2}是等差数列C．{Sn}是等差数列D．{Sn2}是等差数列

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．已知三棱锥A-BCD中，AB=CD=2$\sqrt{13}$，BC=AD=$\sqrt{41}$，AC=BD=$\sqrt{61}$，则三棱锥A-BCD的外接球的表面积为77π．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．双曲线$\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{3}$=1的渐近线方程为（　　）
    A．y=±$\frac{1}{2}$xB．y=±2xC．y=±$\frac{\sqrt{2}}{2}$xD．y=±$\sqrt{2}$x

    查看答案和解析>>

    同步练习册答案