
【题目】甲、乙两位数学老师组队参加某电视台闯关节目,共3关,甲作为嘉宾参与答题,若甲回答错误,乙作为亲友团在整个通关过程中至多只能为甲提供一次帮助机会,若乙回答正确,则甲继续闯关,若某一关通不过,则收获前面所有累积奖金.约定每关通过得到奖金2000元,设甲每关通过的概率为![]() ,乙每关通过的概率为
,乙每关通过的概率为![]() ,且各关是否通过及甲、乙回答正确与否均相互独立.
,且各关是否通过及甲、乙回答正确与否均相互独立.
(1)求甲、乙获得2000元奖金的概率;
(2)设![]() 表示甲、乙两人获得的奖金数,求随机变量
表示甲、乙两人获得的奖金数,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图:
分组的频率分布直方图如图:
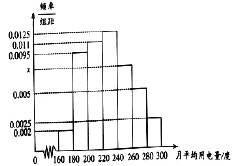
(Ⅰ)求直方图中![]() 的值;
的值;
(Ⅱ)求月平均用电量的众数和中位数;
(Ⅲ)在月平均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在
的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=-3x2+a(6-a)x+6.
(1)解关于a的不等式f(1)>0;
(2)若不等式f(x)>b的解集为(-1,3),求实数a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数y=f(x)对于任意的x都满足f(x+1)=-f(x),当-1≤x<1时,f(x)=x3,若函数g(x)=f(x)-loga|x|至少有6个零点,则a的取值范围是( )
A. ![]() ∪(5,+∞) B.
∪(5,+∞) B. ![]() ∪
∪![]()
C. ![]() ∪(5,7) D.
∪(5,7) D. ![]() ∪[5,7)
∪[5,7)
查看答案和解析>>
科目:高中数学 来源: 题型:
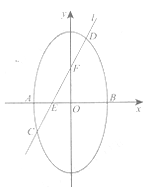
【题目】椭圆![]() 短轴的左右两个端点分别为A,B,直线
短轴的左右两个端点分别为A,B,直线![]() 与x轴、y轴分别交于两点E,F,交椭圆于两点C,D.
与x轴、y轴分别交于两点E,F,交椭圆于两点C,D.
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设直线AD,CB的斜率分别为![]() ,若
,若![]() ,求k的值.
,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
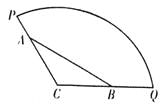
【题目】为方便市民休闲观光,市政府计划在半径为200米,圆心角为![]() 的扇形广场内(如图所示),沿
的扇形广场内(如图所示),沿![]() 边界修建观光道路,其中
边界修建观光道路,其中![]() 分别在线段
分别在线段![]() 上,且
上,且![]() 两点间距离为定长
两点间距离为定长![]() 米.
米.
(1)当![]() 时,求观光道
时,求观光道![]() 段的长度;
段的长度;
(2)为提高观光效果,应尽量增加观光道路总长度,试确定图中![]() 两点的位置,使观光道路总长度达到最长?并求出总长度的最大值.
两点的位置,使观光道路总长度达到最长?并求出总长度的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有外形相同的球分装三个盒子,每盒10个.其中,第一个盒子中7个球标有字母A、3个球标有字母B;第二个盒子中有红球和白球各5个;第三个盒子中则有红球8个,白球2个.试验按如下规则进行:先在第一号盒子中任取一球,若取得标有字母A的球,则在第二号盒子中任取一个球;若第一次取得标有字母B的球,则在第三号盒子中任取一个球.如果第二次取出的是红球,则称试验成功,那么试验成功的概率为( )
A.0.59 B.0.54 C.0.8 D.0.15
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据微信同程旅游的调查统计显示,参与网上购票的1000位购票者的年龄(单位:岁)情况如图所示.
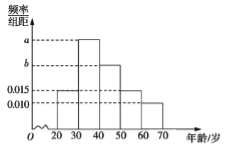
(1)已知中间三个年龄段的网上购票人数成等差数列,求![]() 的值;
的值;
(2)为鼓励大家网上购票,该平台常采用购票就发放酒店入住代金券的方法进行促销,具体做法如下:
年龄在![]() 岁的每人发放20元,其余年龄段的每人发放50元,先按发放代金券的金额采用分层抽样的方式从参与调查的1000位网上购票者中抽取5人,并在这5人中随机抽取3人进行回访调查,求此3人获得代金券的金额总和为90元的概率.
岁的每人发放20元,其余年龄段的每人发放50元,先按发放代金券的金额采用分层抽样的方式从参与调查的1000位网上购票者中抽取5人,并在这5人中随机抽取3人进行回访调查,求此3人获得代金券的金额总和为90元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com