
| A. | (-1,1) | B. | (0,2) | C. | (-$\frac{1}{9}$,$\frac{19}{9}$) | D. | (-$\frac{1}{5}$,$\frac{9}{5}$) |
分析 由绝对值不等式的性质可得-(($\frac{1}{10}$)0+($\frac{1}{10}$)1+…+($\frac{1}{10}$)9)≤f(10)-f(0)≤(($\frac{1}{10}$)0+($\frac{1}{10}$)1+…+($\frac{1}{10}$)9),从而解得.
解答 解:∵|f(n+1)-f(n)|≤($\frac{1}{10}$)n,
∴|f(1)-f(0)|≤($\frac{1}{10}$)0,
|f(2)-f(1)|≤($\frac{1}{10}$)1,
…,
|f(10)-f(9)|≤($\frac{1}{10}$)9,
∴-(($\frac{1}{10}$)0+($\frac{1}{10}$)1+…+($\frac{1}{10}$)9)≤f(10)-f(0)≤(($\frac{1}{10}$)0+($\frac{1}{10}$)1+…+($\frac{1}{10}$)9),
即-$\frac{10}{9}$(1-$\frac{1}{1{0}^{10}}$)≤f(10)-f(0)≤$\frac{10}{9}$(1-$\frac{1}{1{0}^{10}}$),
即-$\frac{10}{9}$<f(10)-f(0)<$\frac{10}{9}$,
故-$\frac{1}{9}$<f(10)<$\frac{19}{9}$,
故选C.
点评 本题考查了绝对值不等式的应用.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:解答题
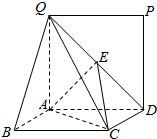 如图,矩形ABCD所在的平面与正方形ADPQ所在的平面相互垂直,E是QD的中点.
如图,矩形ABCD所在的平面与正方形ADPQ所在的平面相互垂直,E是QD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 6 | D. | 2+2$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,3} | B. | {-1,0,1,2,3} | C. | {-1,0,3} | D. | {-1,0} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
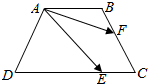 如图,已知ABCD是底角为60°的等腰梯形,其中AB∥CD,AD=4,DC=6,$\overrightarrow{DE}$=2$\overrightarrow{EC}$,$\overrightarrow{CF}$=2$\overrightarrow{FB}$,则$\overrightarrow{AE}$•$\overrightarrow{AF}$的值为$\frac{28}{3}$.
如图,已知ABCD是底角为60°的等腰梯形,其中AB∥CD,AD=4,DC=6,$\overrightarrow{DE}$=2$\overrightarrow{EC}$,$\overrightarrow{CF}$=2$\overrightarrow{FB}$,则$\overrightarrow{AE}$•$\overrightarrow{AF}$的值为$\frac{28}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com