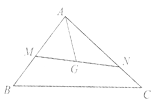
[题目]如右图所示.已知点是的重心.过点作直线与两边分别交于两点.且.则的最小值为 ( )A. 2 B. C. D. 题目和参考答案——青夏教育精英家教网—

【题目】如右图所示，已知点是的重心，过点作直线与两边分别交于两点，且，则的最小值为（）

A. 2 B. C. D.

【答案】C

【解析】因为三点共线，所以，因为是重心，所以，，所以，化简得，解得题目所给图像可知.由基本不等式得

，即.当且仅当，即时，等号成立，故最小值为.

【易错点晴】本题主要考查向量的几何运算及利用基本不等式求最值，属于难题.利用基本不等式求最值时，一定要正确理解和掌握“一正，二定，三相等”的内涵：一正是，首先要判断参数是否为正；二定是，其次要看和或积是否为定值（和定积最大，积定和最小）；三相等是，最后一定要验证等号能否成立（主要注意两点，一是相等时参数否在定义域内，二是多次用或时等号能否同时成立）.

练习册系列答案

赢在中考全程优化单元滚动测试卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】某工厂对一批产品的质量进行了抽样检测，右图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图．已知样本中产品净重在[70，75）克的个数是8个．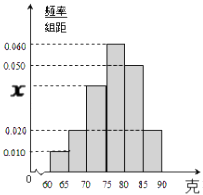
（Ⅰ）求样本容量；
（Ⅱ）若从净重在[60，70）克的产品中任意抽取2个，求抽出的2个产品恰好是净重在[65，70）的产品的概率．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】学校游园活动有这样一个游戏项目：甲箱子里装有3个白球、2个黑球．乙箱子里装有1个白球、2个黑球．每次游戏从这两个箱子里随机摸出2个球，若摸出的白球不少于2个，则获奖．（每次游戏结束后将球放回原箱）
（1）求在1次游戏结束后，①摸出3个白球的概率？②获奖的概率？
（2）求在2次游戏中获奖次数X的分布列及数学期望E（X）．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】为检验寒假学生自主学习的效果，年级部对某班50名学生各科的检测成绩进行了统计，下面是政治成绩的频率分布直方图，其中成绩分组区间是：，，，，，．

（1）求图中的值及平均成绩；

（2）从分数在中选5人记为，从分数在中选3人，记为，8人组成一个学习小组．现从这5人和3人中各选1人做为组长，求被选中且未被选中的概率．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数，其定义域为（）,设．

（Ⅰ）试确定的取值范围,使得函数在上为单调函数；

（Ⅱ）试判断的大小并说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】（本小题满分10分）选修4-4：坐标系与参数方程

已知直线的极坐标方程为，圆的参数方程为

（其中为参数）.

（Ⅰ）将直线的极坐标方程化为直角坐标方程；

（Ⅱ）求圆上的点到直线的距离的最小值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某工厂今年前五个月每月生产某种产品的数量C（件）关于时间t（月）的函数图象如图所示，则这个工厂对这种产品来说（　　）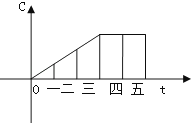

A.一至三月每月生产数量逐月增加，四、五两月每月生产数量逐月减少
B.一至三月每月生产数量逐月增加，四、五月每月生产数量与三月持平
C.一至三月每月生产数量逐月增加，四、五两月均停止生产
D.一至三月每月生产数量不变，四、五两月均停止生产