
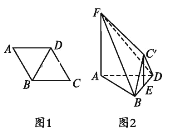
【题目】如图1,在边长为2的菱形![]() 中,
中,![]() ,将
,将![]() 沿对角线
沿对角线![]() 折起到
折起到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 平面
平面![]() ,且
,且![]() ,如图2.
,如图2.
(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成角的余弦值;
所成角的余弦值;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)见解析(2)![]() (3)线段
(3)线段![]() 上不存点
上不存点![]() ,使得
,使得![]() 平面
平面![]() .见解析
.见解析
【解析】
(1)平面![]() 平面
平面![]() ,由面面垂直的性质定理,可证
,由面面垂直的性质定理,可证![]() ,得出
,得出![]() ,即可得证结论;
,即可得证结论;
(2)建立空间直角坐标系,求出平面![]() 的法向量,即可求解;
的法向量,即可求解;
(3)利用共线向量,将![]() 用坐标表示,根据平面
用坐标表示,根据平面![]() 法向量与
法向量与![]() 平面,即可求出结论.
平面,即可求出结论.
(1)证明:∵![]() ,
,![]() 为
为![]() 的中点,∴
的中点,∴![]() .
.
又平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
∴![]() .∵
.∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
而![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
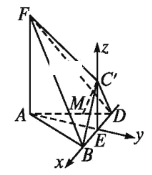
(2)解:以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,
轴,
![]() 所在直线为
所在直线为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
如图所示:则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则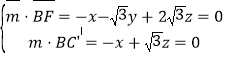 ,
,
取![]() ,则
,则![]() .
.
又平面![]() 的一个法向量为
的一个法向量为![]() ,
,
∴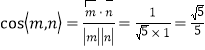 .
.
则平面![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
(3)解:假设在线段![]() 上存在
上存在![]() ,使得
,使得![]() 平面
平面![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,
,![]() ,
,![]() .而
.而![]() .
.
由![]() ,可知
,可知![]() 不存在,
不存在,
∴线段![]() 上不存点
上不存点![]() ,使得
,使得![]() 平面
平面![]() .
.


科目:高中数学 来源: 题型:
【题目】![]() 汉字听写大会
汉字听写大会![]() 不断创收视新高,为了避免“书写危机”,弘扬传统文化,某市大约10万名市民进行了汉字听写测试
不断创收视新高,为了避免“书写危机”,弘扬传统文化,某市大约10万名市民进行了汉字听写测试![]() 现从某社区居民中随机抽取50名市民的听写测试情况,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第1组
现从某社区居民中随机抽取50名市民的听写测试情况,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第1组![]() ,第2组
,第2组![]() ,
,![]() ,第6组
,第6组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.

![]() 若电视台记者要从抽取的市民中选1人进行采访,求被采访人恰好在第2组或第6组的概率;
若电视台记者要从抽取的市民中选1人进行采访,求被采访人恰好在第2组或第6组的概率;
![]() 试估计该市市民正确书写汉字的个数的平均数与中位数;
试估计该市市民正确书写汉字的个数的平均数与中位数;
![]() 已知第4组市民中有3名男性,组织方要从第4组中随机抽取2名市民组成弘扬传统文化宣传队,求至少有1名女性市民的概率.
已知第4组市民中有3名男性,组织方要从第4组中随机抽取2名市民组成弘扬传统文化宣传队,求至少有1名女性市民的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正三角形![]() 的边长为3,
的边长为3,![]() 分别是
分别是![]() 边上的点,满足
边上的点,满足![]() (如图1).将
(如图1).将![]() 折起到
折起到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() ,连接
,连接![]() (如图2).
(如图2).
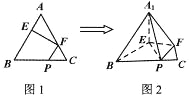
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() .数列
.数列![]() 满足
满足![]() ,
,![]() .
.
(1)若![]() ,且
,且![]() ,求正整数
,求正整数![]() 的值;
的值;
(2)若数列![]() ,
,![]() 均是等差数列,求
均是等差数列,求![]() 的取值范围;
的取值范围;
(3)若数列![]() 是等比数列,公比为
是等比数列,公比为![]() ,且
,且![]() ,是否存在正整数
,是否存在正整数![]() ,使
,使![]() ,
,![]() ,
,![]() 成等差数列,若存在,求出一个
成等差数列,若存在,求出一个![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知两个变量线性相关,若它们的相关性越强,则相关系数的绝对值越接近于1.
(2)线性回归直线必过点![]() ;
;
(3)对于分类变量A与B的随机变量![]() ,
,![]() 越大说明“A与B有关系”的可信度越大.
越大说明“A与B有关系”的可信度越大.
(4)在刻画回归模型的拟合效果时,残差平方和越小,相关指数![]() 的值越大,说明拟合的效果越好.
的值越大,说明拟合的效果越好.
(5)根据最小二乘法由一组样本点![]() ,求得的回归方程是
,求得的回归方程是![]() ,对所有的解释变量
,对所有的解释变量![]() ,
,![]() 的值一定与
的值一定与![]() 有误差.
有误差.
以上命题正确的序号为____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点![]() 作圆
作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,直线
,直线![]() 恰好经过椭圆C:
恰好经过椭圆C:![]() 的右顶点和上顶点.
的右顶点和上顶点.
(1)求椭圆C方程;
(2)过椭圆C左焦点F的直线l交椭圆C于![]() 两点,椭圆上存在一点P,使得四边形
两点,椭圆上存在一点P,使得四边形![]() 为平行四边形,求直线l的方程。
为平行四边形,求直线l的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( ).
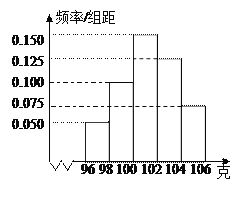
A. 90B. 75C. 60D. 45
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com