
【题目】某共享单车经营企业欲向甲市投放单车,为制定适宜的经营策略,该企业首先在已投放单车的乙市进行单车使用情况调查.调查过程分随机问卷、整理分析及开座谈会三个阶段.在随机问卷阶段,A,B两个调查小组分赴全市不同区域发放问卷并及时收回;在整理分析阶段,两个调查小组从所获取的有效问卷中,针对15至45岁的人群,按比例随机抽取了300份,进行了数据统计,具体情况如下表:
组别 年龄 | A组统计结果 | B组统计结果 | ||
经常使用单车 | 偶尔使用单车 | 经常使用单车 | 偶尔使用单车 | |
| 27人 | 13人 | 40人 | 20人 |
| 23人 | 17人 | 35人 | 25人 |
| 20人 | 20人 | 35人 | 25人 |
(1)先用分层抽样的方法从上述300人中按“年龄是否达到35岁”抽出一个容量为60人的样本,再用分层抽样的方法将“年龄达到35岁”的被抽个体数分配到“经常使用单车”和“偶尔使用单车”中去.求这60人中“年龄达到35岁且偶尔使用单车”的人数;
(2)从统计数据可直观得出“是否经常使用共享单车与年龄(记作![]() 岁)有关”的结论.在用独立性检验的方法说明该结论成立时,为使犯错误的概率尽可能小,年龄
岁)有关”的结论.在用独立性检验的方法说明该结论成立时,为使犯错误的概率尽可能小,年龄![]() 应取25还是35?请通过比较
应取25还是35?请通过比较![]() 的观测值的大小加以说明.
的观测值的大小加以说明.
参考公式:![]() ,其中
,其中![]() .
.
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:
【题目】在我国,大学生就业压力日益严峻,伴随着政府政策引导与社会观念的转变,大学生创业意识,就业方向也悄然发生转变.某大学生在国家提供的税收,担保贷款等很多方面的政策扶持下选择加盟某专营店自主创业,该专营店统计了近五年来创收利润数![]() (单位:万元)与时间
(单位:万元)与时间![]() (单位:年)的数据,列表如下:
(单位:年)的数据,列表如下:

(Ⅰ)依据表中给出的数据,是否可用线性回归模型拟合![]() 与
与![]() 的关系,请计算相关系数
的关系,请计算相关系数![]() 并加以说明(计算结果精确到
并加以说明(计算结果精确到![]() ).(若
).(若![]() ,则线性相关程度很高,可用线性回归模型拟合);
,则线性相关程度很高,可用线性回归模型拟合);
附:相关系数公式

参考数据![]() .
.
(Ⅱ)该专营店为吸引顾客,特推出两种促销方案.
方案一:每满![]() 元可减
元可减![]() 元;
元;
方案二:每满![]() 元可抽奖一次,每次中奖的概率都为
元可抽奖一次,每次中奖的概率都为![]() ,中奖就可以获得
,中奖就可以获得![]() 元现金奖励,假设顾客每次抽奖的结果相互独立.
元现金奖励,假设顾客每次抽奖的结果相互独立.
①某位顾客购买了![]() 元的产品,该顾客选择参加两次抽奖,求该顾客获得
元的产品,该顾客选择参加两次抽奖,求该顾客获得![]() 元现金奖励的概率.
元现金奖励的概率.
②某位顾客购买了![]() 元的产品,作为专营店老板,是希望该顾客直接选择返回
元的产品,作为专营店老板,是希望该顾客直接选择返回![]() 元现金,还是选择参加三次抽奖?说明理由.
元现金,还是选择参加三次抽奖?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知一个动点M在圆![]() 上移动,它与定点
上移动,它与定点![]() 所连线段的中点为P.
所连线段的中点为P.
(1)求点P的轨迹方程.
(2)过定点![]() 的直线与点P的轨迹交于A,B两点,求弦AB的中点C的轨迹.
的直线与点P的轨迹交于A,B两点,求弦AB的中点C的轨迹.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四边形ABCD为梯形,AB∥CD,∠DAB=90°,BDD1B1为矩形,平面BDD1B1⊥平面ABCD,又AB=AD=BB1=1,CD=2.
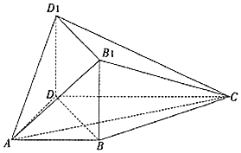
(1)证明:CB1⊥AD1;
(2)求B1到平面ACD1的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
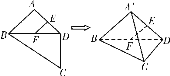
【题目】如图,平面四边形ABCD中,E、F是AD、BD中点,AB=AD=CD=2, BD=2![]() ,∠BDC=90°,将△ABD沿对角线BD折起至△
,∠BDC=90°,将△ABD沿对角线BD折起至△![]() ,使平面
,使平面![]() ⊥平面BCD,则四面体
⊥平面BCD,则四面体![]() 中,下列结论不正确是 ( )
中,下列结论不正确是 ( )
A. EF∥平面![]()
B. 异面直线CD与![]() 所成的角为90°
所成的角为90°
C. 异面直线EF与![]() 所成的角为60°
所成的角为60°
D. 直线![]() 与平面BCD所成的角为30°
与平面BCD所成的角为30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]()
![]() 的长轴长是短轴长的
的长轴长是短轴长的![]() 倍,点
倍,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若过椭圆的左焦点的直线![]() 与椭圆
与椭圆![]() 相交所得弦长为
相交所得弦长为![]() ,求直线
,求直线![]() 的斜率;
的斜率;
(3)过点![]() 的任意直线与椭圆
的任意直线与椭圆![]() 交于
交于![]() 、
、![]() 两点,设点
两点,设点![]() 、
、![]() 到直线
到直线![]() :
:![]() 的距离分别为
的距离分别为![]() .若
.若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com