
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(Ⅰ)判断函数![]() 在
在![]() 内零点的个数,并说明理由;
内零点的个数,并说明理由;
(Ⅱ)![]() ,
,![]() ,使得不等式
,使得不等式![]() 成立,试求实数
成立,试求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若![]() ,求证:
,求证:![]() .
.
【答案】(1)1(2)![]() (3)见解析
(3)见解析
【解析】试题分析:(Ⅰ)首先求函数的导数![]() ,判断导数的正负,得到函数的单调性,再根据零点存在性定理得到零点的个数;(Ⅱ)不等式
,判断导数的正负,得到函数的单调性,再根据零点存在性定理得到零点的个数;(Ⅱ)不等式![]() 等价于
等价于![]() ,根据导数分别求两个函数的最小值和最大值,建立不等式求
,根据导数分别求两个函数的最小值和最大值,建立不等式求![]() 的取值范围;(Ⅲ)利用分析法逐步找到使命题成立的充分条件,即
的取值范围;(Ⅲ)利用分析法逐步找到使命题成立的充分条件,即![]() ,证明
,证明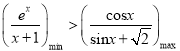 ,求
,求![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)函数![]() 在
在![]() 上的零点的个数为1,,
上的零点的个数为1,,
理由如下:因为![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
所以函数![]() 在
在![]() 上是单调递增函数.
上是单调递增函数.
因为![]() ,
,![]() ,
,
根据函数零点存在性定理得
函数![]() 在
在![]() 上的零点的个数为1.
上的零点的个数为1.
(Ⅱ)因为不等式![]() 等价于
等价于![]() ,
,
所以![]() ,
,![]() ,使得不等式
,使得不等式![]() 成立,等价于
成立,等价于![]() ,
,
当![]() 时,
时,![]() ,故
,故![]() 在区间
在区间![]() 上单调递增,所以
上单调递增,所以![]() 时,
时,![]() 取得最小值-1,
取得最小值-1,
又![]() ,由于
,由于![]() ,
,![]() ,
,![]() ,
,
所以![]() ,故
,故![]() 在区间
在区间![]() 上单调递增.
上单调递增.
因此,![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
所以![]() ,所以
,所以![]() ,
,
所以实数![]() 的取值范围是
的取值范围是![]() .
.
(Ⅲ)当![]() 时,要证
时,要证![]() ,只要证
,只要证![]() ,
,
只要证![]()
![]() ,
,
只要证![]() ,
,
由于![]() ,
,![]() 只要证
只要证![]() .
.
下面证明![]() 时,不等式
时,不等式![]() 成立.
成立.
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 是单调递减;
是单调递减;
当![]() 时,
时,![]() ,
,![]() 是单调递增.
是单调递增.
所以当且仅当![]() 时,
时,![]() 取得极小值也就是最小值为1.
取得极小值也就是最小值为1.
令![]() ,其可看作点
,其可看作点![]() 与点
与点![]() 连线的斜率,
连线的斜率,
所以直线![]() 的方程为:
的方程为:![]() ,
,
由于点![]() 在圆
在圆![]() 上,所以直线
上,所以直线![]() 与圆
与圆![]() 相交或相切,
相交或相切,
当直线![]() 与圆
与圆![]() 相切且切点在第二象限时,
相切且切点在第二象限时,
当直线![]() 取得斜率
取得斜率![]() 的最大值为1.
的最大值为1.
故![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
综上所述,当![]() 时,
时,![]() 成立.
成立.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )(x∈R)的部分图象如图所示.
)(x∈R)的部分图象如图所示.
(Ⅰ)求函数f(x)的解析式并求函数f(x)的单调递增区间;
(Ⅱ)求函数f(x)的最小值并指出函数f(x)取最小值时相应的x的值.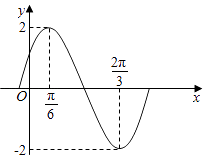
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,已知圆C1:(x+3)2+(y﹣1)2=4和圆C2:(x﹣4)2+(y﹣5)2=4
(1)若直线l过点A(4,0),且被圆C1截得的弦长为2 ![]() ,求直线l的方程
,求直线l的方程
(2)设P为平面上的点,满足:存在过点P的无穷多对互相垂直的直线l1和l2 , 它们分别与圆C1和C2相交,且直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等,求所有满足条件的点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)
某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率。
(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.学#科@网
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电视传媒公司为了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
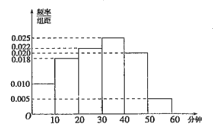
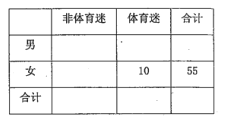
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
(1)根据已知条件完成上面的![]() 列联表,若按
列联表,若按![]() 的可靠性要求,并据此资料,你是否认为“体育迷”与性别有关?
的可靠性要求,并据此资料,你是否认为“体育迷”与性别有关?
(2)将上述调查所得到的频率视为概率.现在从该地区大量电视观众中,采用随机抽样方法每次抽取1名观众,抽取3次,记被抽取的3名观众中的“体育迷”人数为![]() .若每次抽取的结果是相互独立的,求
.若每次抽取的结果是相互独立的,求![]() 分布列,期望
分布列,期望![]() 和方差
和方差![]() .
.
附: 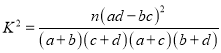

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国历法推测遵循以测为辅、以算为主的原则.例如《周髀算经》和《易经》里对二十四节气的晷影长的记录中,冬至和夏至的晷影长是实测得到的,其他节气的晷影长则是按照等差数列的规律计算得出的.下表为《周髀算经》对二十四节气晷影长的记录,其中![]() 寸表示115寸
寸表示115寸![]() 分(1寸=10分).
分(1寸=10分).
节气 | 冬至 | 小寒(大雪) | 大寒(小雪) | 立春(立冬) | 雨水(霜降) | 惊蛰(寒露) | 春分(秋分) |
晷影长(寸) | 135 |
|
|
|
|
| 75.5 |
节气 | 清明(白露) | 谷雨(处暑) | 立夏(立秋) | 小满(大暑) | 芒种(小暑) | 夏至 | |
晷影长(寸) |
|
|
|
|
| 16.0 |
已知《易知》中记录的冬至晷影长为130.0寸,夏至晷影长为14.8寸,那么《易经》中所记录的惊蛰的晷影长应为__________寸.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com