
【题目】等差数列{an}的公差d≠0满足![]() 成等比数列,若
成等比数列,若![]() =1,Sn是{
=1,Sn是{![]() }的前n项和,则
}的前n项和,则![]() 的最小值为________.
的最小值为________.
【答案】4
【解析】
![]() 成等比数列,
成等比数列,![]() =1,可得:
=1,可得:![]() =
=![]()
![]() ,即(1+2d)2=1+12d,d≠0,解得d.可得an,Sn.代入
,即(1+2d)2=1+12d,d≠0,解得d.可得an,Sn.代入![]() 利用分离常数法化简后,利用基本不等式求出式子的最小值.
利用分离常数法化简后,利用基本不等式求出式子的最小值.
∵![]() 成等比数列,a1=1,
成等比数列,a1=1,
∴![]() =
=![]()
![]() ,
,
∴(1+2d)2=1+12d,d≠0,
解得d=2.
∴an=1+2(n﹣1)=2n﹣1.
Sn=n+![]() ×2=n2.
×2=n2.
∴![]() =
=![]() =n+1+
=n+1+![]() ﹣2≥2
﹣2≥2![]() ﹣2=4,
﹣2=4,
当且仅当n+1=![]() 时取等号,此时n=2,且
时取等号,此时n=2,且![]() 取到最小值4,
取到最小值4,
故答案为:4.
【点睛】
本题考查了等差数列的通项公式、前n项和公式,等比中项的性质,基本不等式求最值,在利用基本不等式求最值时,要特别注意“拆、拼、凑”等技巧,使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用,否则会出现错误.
【题型】填空题
【结束】
17
【题目】设![]() 是公比为正数的等比数列,
是公比为正数的等比数列,![]() ,
,![]()
(1)求![]() 的通项公式;
的通项公式;
(2)设![]() 是首项为1,公差为2的等差数列,求数列
是首项为1,公差为2的等差数列,求数列![]() 的前
的前![]() 项和
项和![]()
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]()
![]() =1,直线l过点M(﹣1,0),与椭圆C交于A,B两点,交y轴于点N.
=1,直线l过点M(﹣1,0),与椭圆C交于A,B两点,交y轴于点N.
(1)设MN的中点恰在椭圆C上,求直线l的方程;
(2)设 ![]() =λ
=λ ![]() ,
, ![]() =μ
=μ ![]() ,试探究λ+μ是否为定值,若是,求出该定值;若不是,请说明理由.
,试探究λ+μ是否为定值,若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
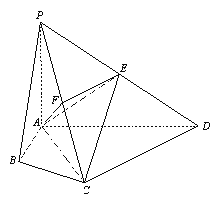
【题目】(14分)在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.
(Ⅰ)求四棱锥P-ABCD的体积V;
(Ⅱ)若F为PC的中点,求证PC⊥平面AEF;
(Ⅲ)求证CE∥平面PAB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-5:不等式选讲]
已知函数f(x)=|x+1|﹣|x﹣2|.
(1)求不等式f(x)≥1的解集;
(2)若不等式f(x)≥x2﹣x+m的解集非空,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形![]() 中,AB∥CD,
中,AB∥CD,![]() ,且
,且![]() .现以
.现以![]() 为一边向梯形外作正方形
为一边向梯形外作正方形![]() ,然后沿边
,然后沿边![]() 将正方形
将正方形![]() 翻折,使平面
翻折,使平面![]() 与平面
与平面![]() 垂直,如图2.
垂直,如图2.


(Ⅰ)求证:BC⊥平面DBE;
(Ⅱ)求点D到平面BEC的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com