
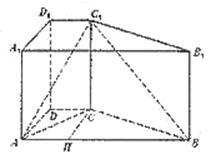
17.[解法一]由题意AB∥DC, ∴∠C1BA是异面直线BC1与DC所成的角。连结AC1与AC,在Rt△ADC中,可得AC=![]() . 又在Rt△ACC1中,可得AC1=3. 在梯形ABCD中,可得AC1=3.在梯形ABCD中,过C作CH∥AD交AB于H,得∠CHB=90°,CH=2, HB=3,
. 又在Rt△ACC1中,可得AC1=3. 在梯形ABCD中,可得AC1=3.在梯形ABCD中,过C作CH∥AD交AB于H,得∠CHB=90°,CH=2, HB=3,
∴CB=![]() ,又在Rt△CBC1中,可得BC1=
,又在Rt△CBC1中,可得BC1=![]() ,
,
 在△ABC1中,cos∠ABC1=
在△ABC1中,cos∠ABC1=![]() .
.
∴∠ABC1=arccos![]() .
.
∴异面直线BC1与DC所成角的大小为arccos![]() .
.
[解法二]如图,以D为坐标原点,分别以DA、DC、DD1所在直线为x、y、z轴建立直角坐标系。
则C1(0,1,2),B(2,4,0),
 ∴
∴![]() =(-2,-3,2),
=(-2,-3,2),
![]() =(0,-1,0),
=(0,-1,0),
设![]() 与
与![]() 所成的角为θ,
所成的角为θ,
则cosθ=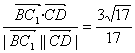 .
.
θ=arccos![]() ,
,
∴异面直线BC1与DC所成角的大小为arccos![]() .
.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com