
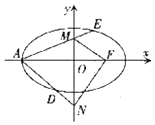
 已知椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左顶点为A,右焦点为F,O为原点,M,N是y轴上的两个动点,且MF⊥NF,直线AM和AN分别与椭圆C交于E,D两点.
已知椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左顶点为A,右焦点为F,O为原点,M,N是y轴上的两个动点,且MF⊥NF,直线AM和AN分别与椭圆C交于E,D两点.分析 (I)F(1,0),设M(0,t1),N(0,t2).不妨设t1>t2.由MF⊥NF,可得$\overrightarrow{MF}$$•\overrightarrow{NF}$=0,化为:t1t2=-1.S△MFN=$\frac{1}{2}(|{t}_{1}|+|{t}_{2}|)$,利用基本不等式的性质即可得出.
(II)A(-$\sqrt{2}$,0).设M(0,t),由(1)可得:N(0,-$\frac{1}{t}$),(t≠±1).直线AM,AN的方程分别为:y=$\frac{t}{\sqrt{2}}$x+t,y=$-\frac{1}{\sqrt{2}t}$x-$\frac{1}{t}$.分别与椭圆方程联立,利用一元二次方程的根与系数的关系可得kOE,kOD.只要证明kOE=kOD.即可得出E,O,D三点共线.
解答 (I)解:F(1,0),设M(0,t1),N(0,t2).不妨设t1>t2.
∵MF⊥NF,∴$\overrightarrow{MF}$$•\overrightarrow{NF}$=1+t1t2=0,化为:t1t2=-1.
∴S△MFN=$\frac{1}{2}×1×|{t}_{1}-{t}_{2}|$=$\frac{1}{2}(|{t}_{1}|+|{t}_{2}|)$≥$\frac{1}{2}×2\sqrt{|{t}_{1}{t}_{2}|}$=1.当且仅当t1=-t2=1时取等号.
∴△MFN的面积的最小值为1.
(II)证明:A(-$\sqrt{2}$,0).
设M(0,t),由(1)可得:N(0,-$\frac{1}{t}$),(t≠±1).
直线AM,AN的方程分别为:y=$\frac{t}{\sqrt{2}}$x+t,y=$-\frac{1}{\sqrt{2}t}$x-$\frac{1}{t}$.
联立$\left\{\begin{array}{l}{y=\frac{t}{\sqrt{2}}x+t}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,化为:(1+t2)x2+2$\sqrt{2}$t2x+2t2-2=0,
∴-$\sqrt{2}$xE=$\frac{2{t}^{2}-2}{1+{t}^{2}}$,可得xE=$\frac{\sqrt{2}-\sqrt{2}{t}^{2}}{1+{t}^{2}}$,yE=$\frac{t}{\sqrt{2}}$×$\frac{\sqrt{2}-\sqrt{2}{t}^{2}}{1+{t}^{2}}$+t=$\frac{2t}{1+{t}^{2}}$,可得kOE=$\frac{\sqrt{2}t}{1-{t}^{2}}$.
联立$\left\{\begin{array}{l}{y=-\frac{1}{\sqrt{2}t}x-\frac{1}{t}}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,化为:(1+t2)x2+2$\sqrt{2}$x+2-2t2=0,
可得:$-\sqrt{2}$xD=$\frac{2-2{t}^{2}}{1+{t}^{2}}$,解得xD=$\frac{\sqrt{2}({t}^{2}-1)}{1+{t}^{2}}$,yD=$-\frac{1}{\sqrt{2}t}$×$\frac{\sqrt{2}({t}^{2}-1)}{1+{t}^{2}}$-$\frac{1}{t}$=$\frac{-2t}{1+{t}^{2}}$,可得kOD=$\frac{\sqrt{2}t}{1-{t}^{2}}$.
∴kOE=kOD.
∴E,O,D三点共线.
点评 本题考查了直线与椭圆相交问题、一元二次方程的根与系数的关系、斜率与三点共线关系、向量垂直与数量积的关系,考查了推理能力与计算能力,属于难题.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
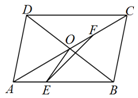 已知平行四边形ABCD中,$|\overrightarrow{AB}|=3$,$|\overrightarrow{AD}|=2$,对角线AC交BD于点O,AB上一点E满足$\overrightarrow{OE}•\overrightarrow{BD}=0$,F为AC上任意一点.
已知平行四边形ABCD中,$|\overrightarrow{AB}|=3$,$|\overrightarrow{AD}|=2$,对角线AC交BD于点O,AB上一点E满足$\overrightarrow{OE}•\overrightarrow{BD}=0$,F为AC上任意一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 我国古代,9是数字之极,代表尊贵之意,所以中国古代皇家建筑中包含许多与9相关的设计.例如,北京天坛圆丘的地面由扇环形的石板铺成(如图所示),最高一层是一块天心石,围绕它的第一圈有9块石板,从第二圈开始,每一圈比前一圈多9块,共有9圈,则前9圈的石板总数是405.
我国古代,9是数字之极,代表尊贵之意,所以中国古代皇家建筑中包含许多与9相关的设计.例如,北京天坛圆丘的地面由扇环形的石板铺成(如图所示),最高一层是一块天心石,围绕它的第一圈有9块石板,从第二圈开始,每一圈比前一圈多9块,共有9圈,则前9圈的石板总数是405.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com