【题目】已知等差数列{an}，a2=8，前9项和为153．
（1）求a5和an；
（2）若 
，证明数列{bn}为等比数列；
【答案】
（1）
设数列{an}的公差为d，首项 
，则 
∴ 
∴a5=17．∵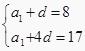 
， 
∴an=3n+2．
（2）
，∴数列{bn}是首项为32，公比为8的等比数列
【解析】知识点：等差数列的通项公式 等比关系的确定
解析 （1）根据前9项和为153和第五项是前9项的等差中项，得到第五项的值，根据第二项和第五项的值列出方程求得首项和公差，写出通项公式．（2）要证明数列是等比数列，只要相邻两项之比是常数即可，两项之比是一个常数得到结论．
【考点精析】解答此题的关键在于理解等差数列的通项公式（及其变式）的相关知识，掌握通项公式：
或
，以及对等差关系的确定的理解，了解如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，即
－
=d ，（n≥2，n∈N
）那么这个数列就叫做等差数列．
举一反三单元同步过关卷系列答案科目：高中数学 来源： 题型：
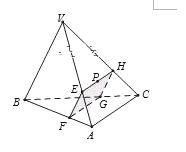
【题目】如图所示，在四面体VABC木块中，P为△VAC的重心，这点P作截面EFGH，若截面EFGH是平行四边形，则该截面把木块分成两部分体积之比为____________． （填体积小与体积大之比）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，2012年春节，摄影爱好者
在某公园
处，发现正前方
处有一立柱，测得立柱顶端
的仰角和立柱底部
的俯角均为
，设
的眼睛距地面的距离
米.
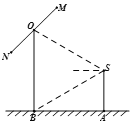
（1）求摄影者到立柱的水平距离和立柱的高度；
（2）立柱的顶端有一长2米的彩杆
绕其中点
在
与立柱所在的平面内旋转．摄影者有一视角范围为
的镜头，在彩杆转动的任意时刻，摄影者是否都可以将彩杆全部摄入画面？说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设f（x）＝（1﹣m）lnx+
+nx（m，n是常数）．
（1）若m＝0，且f（x）在（1，2）上单调递减，求n的取值范围；
（2）若m＞0，且n＝﹣1，求f（x）的单调区间．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如果数列a1 ， a2 ， a3 ， … ， an ， …是等差数列，那么下列数列中不是等差数列的是：（ ）
A.a1+x ， a2+x ， a3+x ， …，an+x ，
B.ka1 ， ka2 ， ka3 ， …，kan ，
C.
D.a1 ， a4 ， a7 ， …a3n﹣2 ，
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在数列{an}中，已知a1= 
，an+1= an﹣ 
，n∈N* ， 设Sn为{an}的前n项和．
（1）求证：数列{3nan}是等差数列；
（2）求Sn；
（3）是否存在正整数p，q，r（p＜q＜r），使Sp ， Sq ， Sr成等差数列？若存在，求出p，q，r的值；若不存在，说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
