
【题目】由经验得知,在某商场付款处排队等候付款的人数及概率如表:
排队人数 |
|
|
|
|
|
|
概率 |
|
|
|
|
|
|
(1)至多有![]() 人排队的概率是多少?
人排队的概率是多少?
(2)至少有![]() 人排队的概率是多少?
人排队的概率是多少?
【答案】(1)0.56(2)0.74
【解析】分析:(1)“至多2人排队”是“没有人排队”,“1人排队”,“2人排队”三个事件的和事件,三个事件彼此互斥,利用互斥事件的概率公式求出“至多2人排队”的概率;
(2)“至少2人排队”与“少于2人排队”是对立事件,“少于2人排队”是“没有人排队”,“1人排队”两个事件的和事件,这两个事件彼此互斥,利用互斥事件的概率公式求出“少于2人排队”的概率;再利用对立事件的概率公式求出“至少2人排队”的概率.
详解:(1)记没有人排队为事件A,1人排队为事件B.2人排队为事件C,A、B、C彼此互斥.所以P(A+B+C)=P(A)+P(B)+P(C)=0.1+0.16+0.3=0.56;
(2)记至少2人排队为事件D,少于2人排队为事件A+B,那么事件D与A+B是对立事件,
则P(D)=P(![]() )=1﹣(P(A)+P(B))=1﹣(0.1+0.16)=0.74.
)=1﹣(P(A)+P(B))=1﹣(0.1+0.16)=0.74.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:
【题目】平面直角坐标系 ![]() 中,倾斜角为
中,倾斜角为 ![]() 的直线
的直线 ![]() 过点
过点 ![]() ,以原点
,以原点 ![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线 ![]() 的极坐标方程为
的极坐标方程为 ![]() .
.
(1)写出直线 ![]() 的参数方程(
的参数方程( ![]() 为常数)和曲线
为常数)和曲线 ![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线 ![]() 与
与 ![]() 交于
交于 ![]() 、
、 ![]() 两点,且
两点,且 ![]() ,求倾斜角
,求倾斜角 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生对函数![]() 的性质进行研究,得出如下的结论:
的性质进行研究,得出如下的结论:
①函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
②点![]() 是函数
是函数![]() 图像的一个对称中心;
图像的一个对称中心;
③存在常数![]() ,使
,使![]() 对一切实数
对一切实数![]() 均成立;
均成立;
④函数![]() 图像关于直线
图像关于直线![]() 对称.其中正确的结论是__________.
对称.其中正确的结论是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,且将全班![]() 人的成绩记为
人的成绩记为![]() 由右边的程序运行后,输出
由右边的程序运行后,输出![]() .据此解答如下问题:
.据此解答如下问题:
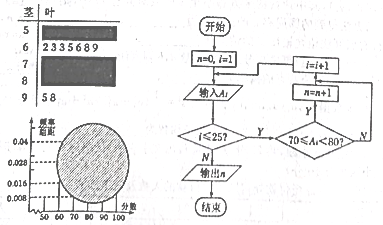
注:图中![]() 表示“是”,
表示“是”,![]() 表示“否”
表示“否”
(1)求茎叶图中破损处分数在![]() ,
,![]() ,
,![]() 各区间段的频数;
各区间段的频数;
(2)利用频率分布直方图估计该班的数学测试成绩的众数,中位数分别是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形 ![]() 中,
中, ![]() ,点
,点 ![]() 为
为 ![]() 的中点,
的中点, ![]() 为线段
为线段 ![]() (端点除外)上一动点.现将
(端点除外)上一动点.现将 ![]() 沿
沿 ![]() 折起,使得平面
折起,使得平面 ![]() 平面
平面 ![]() .设直线
.设直线 ![]() 与平面
与平面 ![]() 所成角为
所成角为 ![]() ,则
,则 ![]() 的最大值为( )
的最大值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明家订了一份报纸,送报人可能在早上6 : 30至7 : 30之间把报纸送到小明家,小明离开家去上学的时间在早上7 : 00至8 : 30之间,问小明在离开家前能得到报纸(称为事件![]() )的概率是多少( )
)的概率是多少( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C: ![]() 的右顶点为A,离心率为e,且椭圆C过点
的右顶点为A,离心率为e,且椭圆C过点 ![]() ,以AE为直径的圆恰好经过椭圆的右焦点.
,以AE为直径的圆恰好经过椭圆的右焦点.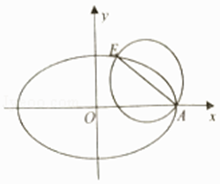
(1)求椭圆C的标准方程;
(2)已知动直线l(直线l不过原点且斜率存在)与椭圆C交于P,Q两个不同的点,且△OPQ的面积S=1,若N为线段PQ的中点,问:在x轴上是否存在两个定点E1 , E2 , 使得直线NE1与NE2的斜率之积为定值?若存在,求出E1 , E2的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com