
【题目】为缓解堵车现象,解决堵车问题,银川市交警队调查了甲乙两个路口的车流量,在2019年6月随机选取了14天,统计每天上午7:30-9:00早高峰时段各自的车流量(单位:百辆)得到如图所示的茎叶图,根据茎叶图回答以下问题.

(1)甲乙两个路口的车流量的中位数分别是多少?
(2)试计算甲乙两个路口的车流量在![]() 之间的频率.
之间的频率.
科目:高中数学 来源: 题型:
【题目】袋中装有红球3个、白球2个、黑球1个,从中任取2个,则互斥而不对立的两个事件是![]()
![]()
A. 至少有一个白球;都是白球 B. 至少有一个白球;至少有一个红球
C. 至少有一个白球;红、黑球各一个 D. 恰有一个白球;一个白球一个黑球
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数
上是增函数![]() 若函数
若函数![]() ,利用上述性质,
,利用上述性质,
![]() Ⅰ
Ⅰ![]() 当
当![]() 时,求
时,求![]() 的单调递增区间
的单调递增区间![]() 只需判定单调区间,不需要证明
只需判定单调区间,不需要证明![]() ;
;
![]() Ⅱ
Ⅱ![]() 设
设![]() 在区间
在区间![]() 上最大值为
上最大值为![]() ,求
,求![]() 的解析式;
的解析式;
![]() Ⅲ
Ⅲ![]() 若方程
若方程![]() 恰有四解,求实数a的取值范围.
恰有四解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年11月3日20点43分我国长征运载火箭在海南文昌发射中心成功发射,它被公认为我国已从航天大国向航天强国迈进的重要标志.长征五号运载火箭的设计生产采用很多新材料,甲工厂承担了某种材料的生产,并以![]() 千克/时的速度匀速生产(为保证质量要求
千克/时的速度匀速生产(为保证质量要求![]() ),每小时可消耗
),每小时可消耗![]() 材料
材料![]() 千克,已知每小时生产1千克该产品时,消耗
千克,已知每小时生产1千克该产品时,消耗![]() 材料10千克.
材料10千克.
(1)设生产![]() 千克该产品,消耗
千克该产品,消耗![]() 材料
材料![]() 千克,试把
千克,试把![]() 表示为
表示为![]() 的函数.
的函数.
(2)要使生产1000千克该产品消耗的![]() 材料最少,工厂应选取何种生产速度?并求消耗的
材料最少,工厂应选取何种生产速度?并求消耗的![]() 材料最少为多少?
材料最少为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一块矩形空地,要在这块空地上开辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知![]() 且
且![]() 设
设![]() ,绿地面积为
,绿地面积为![]() .
.
(1)写出![]() 关于
关于![]() 的函数关系式,并指出这个函数的定义域.
的函数关系式,并指出这个函数的定义域.
(2)当![]() 为何值时,绿地面积
为何值时,绿地面积![]() 最大?
最大?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求使不等式
,求使不等式![]() 对一切
对一切![]() 都成立的正整数
都成立的正整数![]() 的最大值.
的最大值.
(3)设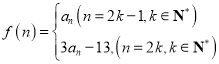 ,是否存在
,是否存在![]() ,使得
,使得![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】首届世界低碳经济大会在南昌召开,本届大会以“节能减排,绿色生态”为主题,某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可近似地表示为
(吨)之间的函数关系可近似地表示为![]() ,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则需要国家至少补贴多少元才能使该单位不亏损?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是线段
是线段![]() 上异于端点的一点,平面
上异于端点的一点,平面![]()
![]() 平面
平面![]() ,
,![]() .
.

(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】巳知集合P={![]() },Q={
},Q={![]() },将P∪Q的所有元素从小到大依次排列构成一个数列{
},将P∪Q的所有元素从小到大依次排列构成一个数列{![]() },记
},记![]() 为数列{
为数列{![]() }的前n项和,则使得
}的前n项和,则使得![]() <1000成立的
<1000成立的![]() 的最大值为
的最大值为
A. 9 B. 32 C. 35 D. 61
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com