设函数f(x)=x3+ax2-a2x+m(a≥0).
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若函数f(x)在x∈[-1,1]内没有极值点,求a的取值范围;
(Ⅲ)若对任意的a∈[3,6),不等式f(x)≤1在x∈[-2,2]上恒成立,求m的取值范围.
解:(Ⅰ)∵f'(x)=3x
2+2ax-a
2=
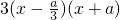
当a=0时f′(x)≥0
∴函数f(x)的单调递增区间为(-∞,+∞)
当a>0时
由f′(x)>0得x<-a或
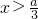
,
由f′(x)<0得

,
∴函数f(x)的单调递增区间为(-∞,-a),
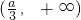
,
单调递减区间为

(Ⅱ)当a=0时由(1)知函数f(x)在[-1,1]上单调递增,
则f(x)在[-1,1]上没有极值点;
当a>0时∵
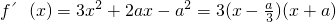
由(1)知f(x)在
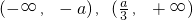
上单调递增,
在

上单调递减;则要f(x)在[-1,1]上没有极值点,
则只需f′(x)=0在(-1,1)上没有实根.∴
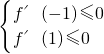
,解得a≥3
综上述可知:a的取值范围为[3,+∞)∪{0}
(Ⅲ)∵a∈[3,6),
∴
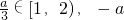
≤-3
又x∈[-2,2]
由(1)的单调性质知f(x)
max=max{f(-2),f(2)}
而f(2)-f(-2)=16-4a
2<0
∴f(x)
max=f(-2)=-8+4a+2a
2+m
∵f(x)≤1在[-2,2]上恒成立
∴f(x)
max≤1即-8+4a+2a
2+m≤1
即m≤9-4a-2a
2在a∈[3,6]上恒成立,
∵9-4a-2a
2的最小值为-87
∴m≤-87
故答案为(Ⅰ)当a=0时f′(x)≥0,
函数f(x)的单调递增区间为(-∞,+∞),
当a>0时函数f(x)的单调递增区间为
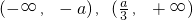
,
单调递减区间为

,
(Ⅱ)a的取值范围为:[3,+∞)∪{0},
(Ⅲ)m的取值范围为:m≤-87.
分析:(Ⅰ)要求函数f(x)的单调区间,即求函数f(x)的f′(x),在根据导数与单调性的关系求解即可
(Ⅱ)要使函数f(x)在x∈[-1,1]内没有极值点,只需f′(x)=0在(-1,1)上没有实根即可
(Ⅲ)要求对任意的a∈[3,6),不等式f(x)≤1在x∈[-2,2]上恒成立,只需求当x∈[-2,2]时f(x)
max≤1,即m≤9-4a-2a
2在a∈[3,6]上恒成立,即求9-4a-2a
2在a∈[3,6]的最小值.
点评:本题考查了利用导数求闭区间上函数的最值,利用导数研究函数的单调性,函数在某点取得极值的条件,还考查了变量分离的思想方法,属于基础题.

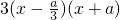
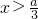 ,
, ,
,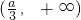 ,
,
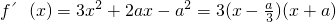
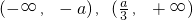 上单调递增,
上单调递增, 上单调递减;则要f(x)在[-1,1]上没有极值点,
上单调递减;则要f(x)在[-1,1]上没有极值点,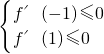 ,解得a≥3
,解得a≥3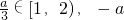 ≤-3
≤-3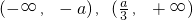 ,
, ,
,
