
【题目】一个国际象棋棋盘(由8×8个方格组成),其中有一个小方格因破损而被剪去(破损位置不确定).“L”形骨牌由三个相邻的小方格组成,如图所示.现要将这个破损的棋盘剪成数个“L”形骨牌,则( )
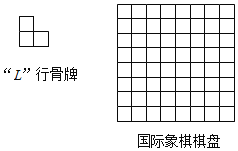
A.至多能剪成19块“L”形骨牌
B.至多能剪成20块“L”形骨牌
C.最多能剪成21块“L”形骨牌
D.前三个答案都不对
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
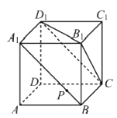
【题目】如图,在正方体![]() 中,点
中,点![]() 在线段
在线段![]() 上移动,有下列判断:①平面
上移动,有下列判断:①平面![]() 平面
平面![]() ;②平面
;②平面![]() 平面
平面![]() ;③三棱锥
;③三棱锥![]() 的体积不变;④
的体积不变;④![]() 平面
平面![]() .其中,正确的是______.(把所有正确的判断的序号都填上)
.其中,正确的是______.(把所有正确的判断的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
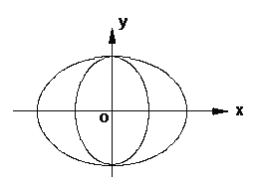
【题目】如图,曲线![]() 由两个椭圆
由两个椭圆![]() :
:![]() 和椭圆
和椭圆![]() :
:![]() 组成,当
组成,当![]() 成等比数列时,称曲线
成等比数列时,称曲线![]() 为“猫眼曲线”.
为“猫眼曲线”.
(1)若猫眼曲线![]() 过点
过点![]() ,且
,且![]() 的公比为
的公比为![]() ,求猫眼曲线
,求猫眼曲线![]() 的方程;
的方程;
(2)对于题(1)中的求猫眼曲线![]() ,任作斜率为
,任作斜率为![]() 且不过原点的直线与该曲线相交,交椭圆
且不过原点的直线与该曲线相交,交椭圆![]() 所得弦的中点为M,交椭圆
所得弦的中点为M,交椭圆![]() 所得弦的中点为N,求证:
所得弦的中点为N,求证:![]() 为与
为与![]() 无关的定值;
无关的定值;
(3)若斜率为![]() 的直线
的直线![]() 为椭圆
为椭圆![]() 的切线,且交椭圆
的切线,且交椭圆![]() 于点
于点![]() ,
,![]() 为椭圆
为椭圆![]() 上的任意一点(点
上的任意一点(点![]() 与点
与点![]() 不重合),求
不重合),求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,对于点
中,对于点![]() ,定义变换
,定义变换![]() :将点
:将点![]() 变换为点
变换为点![]() ,使得
,使得![]() 其中
其中![]() .这样变换
.这样变换![]() 就将坐标系
就将坐标系![]() 内的曲线变换为坐标系
内的曲线变换为坐标系![]() 内的曲线.则四个函数
内的曲线.则四个函数![]() ,
,![]() ,
,![]() ,
,![]() 在坐标系
在坐标系![]() 内的图象,变换为坐标系
内的图象,变换为坐标系![]() 内的四条曲线(如图)依次是
内的四条曲线(如图)依次是
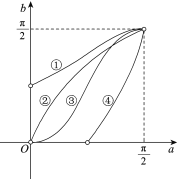
A. ②,③,①,④B. ③,②,④,①C. ②,③,④,①D. ③,②,①,④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() 是一个集合,
是一个集合,![]() 是一个以
是一个以![]() 的某些子集为元素的集合,且满足:(1)
的某些子集为元素的集合,且满足:(1)![]() 属于
属于![]() ,
,![]() 属于
属于![]() ;(2)
;(2)![]() 中任意多个元素的并集属于
中任意多个元素的并集属于![]() ;(3)
;(3)![]() 中任意多个元素的交集属于
中任意多个元素的交集属于![]() ,则称
,则称![]() 是集合
是集合![]() 上的一个拓补.已知集合
上的一个拓补.已知集合![]() ,对于下面给出的四个集合
,对于下面给出的四个集合![]() :
:
①![]() ②
②![]()
③![]() ④
④![]()
其中是集合![]() 上的拓补的集合
上的拓补的集合![]() 的序号是______.(写出所有的拓补的集合
的序号是______.(写出所有的拓补的集合![]() 的序号)
的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】德阳中学数学竞赛培训共开设有初等代数、初等几何、初等数论和微积分初步共四门课程,要求初等代数、初等几何都要合格,且初等数论和微积分初步至少有一门合格,则能取得参加数学竞赛复赛的资格,现有甲、乙、丙三位同学报名参加数学竞赛培训,每一位同学对这四门课程考试是否合格相互独立,其合格的概率均相同,(见下表),且每一门课程是否合格相互独立,
课 程 | 初等代数 | 初等几何 | 初等数论 | 微积分初步 |
合格的概率 |
|
|
|
|
(1)求甲同学取得参加数学竞赛复赛的资格的概率;
(2)记![]() 表示三位同学中取得参加数学竞赛复赛的资格的人数,求
表示三位同学中取得参加数学竞赛复赛的资格的人数,求![]() 的分布列及期望
的分布列及期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是由正方形![]() ,直角梯形
,直角梯形![]() ,三角形
,三角形![]() 组成的一个平面图形,其中
组成的一个平面图形,其中![]() ,
,![]() ,将其沿
,将其沿![]() ,
,![]() 折起使得
折起使得![]() 与
与![]() 重合,连接
重合,连接![]() ,如图2.
,如图2.
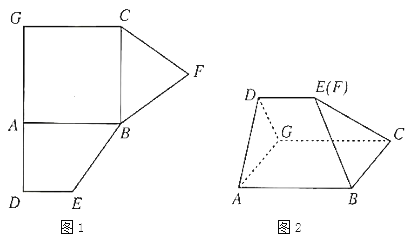
(1)证明:图2中的![]() ,
,![]() ,
,![]() ,
,![]() 四点共面,且平面
四点共面,且平面![]() 平面
平面![]() ;
;
(2)求图2中的二面角![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com