
【题目】已知函数![]() .
.
(1)若![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,![]() 有两个不同的零点
有两个不同的零点![]() ,求证:
,求证:![]() .
.
科目:高中数学 来源: 题型:
【题目】某农场灌溉水渠长为1000米,横截面是等腰梯形,如图,在等腰梯形![]() 中,
中,![]() ,
,![]() ,其中渠底
,其中渠底![]() 宽为1米,渠口
宽为1米,渠口![]() 宽为3米,渠深
宽为3米,渠深![]() 米.根据国家对农田建设补贴的政策,该农场计划在原水渠的基础上分别沿射线
米.根据国家对农田建设补贴的政策,该农场计划在原水渠的基础上分别沿射线![]() 方向加宽、
方向加宽、![]() 方向加深,若扩建后的水渠横截面
方向加深,若扩建后的水渠横截面![]() 仍是等腰梯形,且面积是原面积的2倍.设扩建后渠深为
仍是等腰梯形,且面积是原面积的2倍.设扩建后渠深为![]() 米,若挖掘费用为每立方米
米,若挖掘费用为每立方米![]() 万元,水渠的内壁(渠底和梯形两腰,
万元,水渠的内壁(渠底和梯形两腰,![]() 端也要重新铺设)铺设混凝土的费用为每平方米
端也要重新铺设)铺设混凝土的费用为每平方米![]() 万元.
万元.

(1)用![]() 表示渠底
表示渠底![]() 的长度,并求出
的长度,并求出![]() 的取值范围;
的取值范围;
(2)问渠深![]() 为多少米时,建设费用最低?
为多少米时,建设费用最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某射击运动员在比赛前进行三周的封闭训练,教练员将其每天成绩的均值数据整理,并绘成条形图如下,
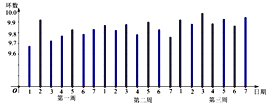
根据该图,下列说法错误的是:( )
A.第三周平均成绩最好B.第一周平均成绩比第二平均成绩好
C.第一周成绩波动较大D.第三周成绩比较稳定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某周末,郑州方特梦幻王国汇聚了八方来客.面对该园区内相邻的两个主题公园“千古蝶恋”和“西游传说”,成年人和未成年人选择游玩的意向会有所不同.某统计机构对园区内的100位游客(这些游客只在两个主题公园中二选一)进行了问卷调查.调查结果显示,在被调查的50位成年人中,只有10人选择“西游传说”,而选择“西游传说”的未成年人有20人.
(1)根据题意,请将下面的![]() 列联表填写完整;
列联表填写完整;
选择“西游传说” | 选择“千古蝶恋” | 总计 | |
成年人 | |||
未成年人 | |||
总计 |
(2)根据列联表的数据,判断是否有![]() 的把握认为选择哪个主题公园与年龄有关.
的把握认为选择哪个主题公园与年龄有关.
附参考公式与表: (
(![]() ).
).
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
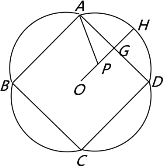
【题目】如图是一幅招贴画的示意图,其中ABCD是边长为![]() 的正方形,周围是四个全等的弓形.已知O为正方形的中心,G为AD的中点,点P在直线OG上,弧AD是以P为圆心、PA为半径的圆的一部分,OG的延长线交弧AD于点H.设弧AD的长为
的正方形,周围是四个全等的弓形.已知O为正方形的中心,G为AD的中点,点P在直线OG上,弧AD是以P为圆心、PA为半径的圆的一部分,OG的延长线交弧AD于点H.设弧AD的长为![]() ,
,![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)定义比值![]() 为招贴画的优美系数,当优美系数最大时,招贴画最优美.证明:当角
为招贴画的优美系数,当优美系数最大时,招贴画最优美.证明:当角![]() 满足:
满足:![]() 时,招贴画最优美.
时,招贴画最优美.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R的奇函数![]() 满足
满足![]() ,且
,且![]() 时,
时, ![]() ,下面四种说法①
,下面四种说法①![]() ;②函数
;②函数![]() 在[-6,-2]上是增函数;③函数
在[-6,-2]上是增函数;③函数![]() 关于直线
关于直线![]() 对称;④若
对称;④若![]() ,则关于
,则关于![]() 的方程
的方程![]() 在[-8,8]上所有根之和为-8,其中正确的序号__________。
在[-8,8]上所有根之和为-8,其中正确的序号__________。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春季,某出租汽车公司决定更换一批新的小汽车以代替原来报废的出租车,现有![]() 两款车型,根据以往这两种出租车车型的数据,得到两款出租车车型使用寿命频数表如下:
两款车型,根据以往这两种出租车车型的数据,得到两款出租车车型使用寿命频数表如下:
使用寿命年数 | 5年 | 6年 | 7年 | 8年 | 总计 |
| 10 | 20 | 45 | 25 | 100 |
| 15 | 35 | 40 | 10 | 100 |
(1)填写下表,并判断是否有![]() 的把握认为出租车的使用寿命年数与汽车车型有关?
的把握认为出租车的使用寿命年数与汽车车型有关?
使用寿命不高于 | 使用寿命不低于 | 总计 | |
| |||
| |||
总计 |
(2)司机师傅小李准备在一辆开了![]() 年的
年的![]() 型车和一辆开了
型车和一辆开了![]() 年的
年的![]() 型车中选择,为了尽最大可能实现
型车中选择,为了尽最大可能实现![]() 年内(含
年内(含![]() 年)不换车,试通过计算说明,他应如何选择.
年)不换车,试通过计算说明,他应如何选择.
附: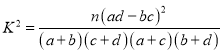 ,
,![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为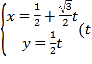 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com