【题目】设0<a<1，则函数f(x)＝loga|
|（ ）
A.在(－∞，－1)和(1，＋∞)上单调递减，在(－1,1)上单调递增
B.在(－∞，－1)和(1，＋∞)上单调递增，在(－1,1)上单调递减
C.在(－∞，－1)和(1，＋∞)上单调递增，在(－1,1)上单调递增
D.在(－∞，－1)和(1，＋∞)上单调递减，在(－1,1)上单调递减
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案科目：高中数学 来源： 题型：
【题目】某校从参加某次知识竞赛测试的学生中随机抽出60名学生，将其成绩（百分制）（均为整数）分成六段
，
…
后得到如下部分频率分布直方图.观察图形的信息，回答下列问题：
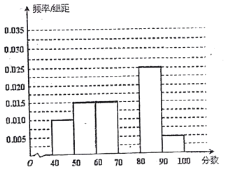
（1）求分数在
内的频率，并补全这个频率分布直方图；
（2）根据频率分布直方图，从图中估计总体的众数是多少分？中位数是多少分？
（3）统计方法中，同一组数据常用该组区间的中点值作为代表，据此估计本次考试的平均分.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列叙述中正确的是（ ）
A. 若
，则“
”的充分条件是“
”
B. 若，则“
”的充要条件是“
”
C. 命题“
”的否定是“
”
D. 
是等比数列，则
是为单调递减数列的充分条件
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝excos x－x.
(1)求曲线y＝f(x)在点(0，f(0))处的切线方程；
(2)求函数f(x)在区间
上的最大值和最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
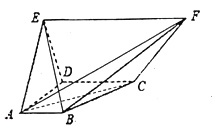
【题目】在图所示的五面体中，面ABCD为直角梯形，
，平面
平面ABCD，
，
，
是边长为2的正三角形．
证明：
平面ACF；
若点P在线段EF上，且二面角
的余弦值为
，求
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知f(x)是R上的奇函数，且当x>0时，f(x)＝－x2＋2x＋2.
(1)求f(x)的解析式；
(2)画出f(x)的图像，并指出f(x)的单调区间．
查看答案和解析>>
科目：高中数学 来源： 题型：
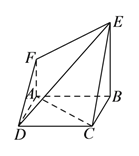
【题目】在如图所示的几何体中，四边形
为正方形，四边形
为直角梯形，且
， 
，平面
平面
， 
．
（
）求证： 
平面
．
（
）若二面角
为直二面角，
（i）求直线
与平面
所成角的大小．
（ii）棱
上是否存在点
，使得
平面
？若存在，求出
的值；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图,一张矩形白纸ABCD,AB=10,AD=
,E,F分别为AD,BC的中点,现分别将△ABE,△CDF沿BE,DF折起,且A、C在平面BFDE同侧,下列命题正确的是____________(写出所有正确命题的序号)
①当平面ABE∥平面CDF时,AC∥平面BFDE
②当平面ABE∥平面CDF时,AE∥CD
③当A、C重合于点P时,PG⊥PD
④当A、C重合于点P时,三棱锥P-DEF的外接球的表面积为150
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=x2+bx+c，其中b，c∈R．
（1）当f（x）的图象关于直线x=1对称时，b=______；
（2）如果f（x）在区间[-1，1]不是单调函数，证明：对任意x∈R，都有f（x）＞c-1；
（3）如果f（x）在区间（0，1）上有两个不同的零点．求c2+（1+b）c的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
