
设△ABC三个角A,B,C的对边分别为a,b,c,向量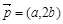 ,
, ,且
,且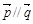 .
.
(Ⅰ)求角B的大小;
(Ⅱ)若△ABC是锐角三角形,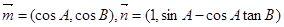 ,求
,求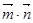 的取值范围.
的取值范围.
(Ⅰ)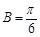 或
或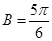 .(Ⅱ)
.(Ⅱ)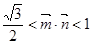 .
.
【解析】
试题分析:(Ⅰ)∵ 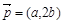 ,
,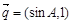 ,且
,且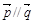 ,
,
∴ a-2bsinA = 0,由正弦定理得 sinA-2sinB sinA = 0. 3分
∵ 0<A,B,C<p,∴ 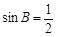 ,得
,得 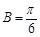 或
或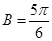 .
5分
.
5分
(Ⅱ)∵ △ABC是锐角三角形,∴ 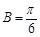 ,
-6分
,
-6分
∴ 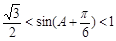 ,即
,即 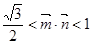 .
-12分
.
-12分
考点:平面向量的坐标运算,向量平行的条件,正弦定理的应用,两角和差的三角函数,三角函数的性质。
点评:中档题,本题难度不大,但考查知识较为全面,综合考查了平面向量的坐标运算,向量平行的条件,正弦定理的应用,两角和差的三角函数,三角函数的性质。在三角形中,角的范围受到了限制,确定三角函数值范围时,要特别注意。


科目:高中数学 来源: 题型:
| p |
| q |
| p |
| q |
| m |
| n |
| m |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| 7 |
| m |
| n |
| m |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| tanB |
| tanA |
| 2c | ||
|
| m |
| n |
| m |
| n |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三第七次阶段复习达标检测理科数学试卷(解析版) 题型:解答题
设△ABC三个角A,B,C的对边分别为a,b,c,向量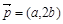 ,
,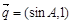 ,且
,且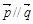 .
.
(Ⅰ)求角B的大小;
(Ⅱ)若△ABC是锐角三角形,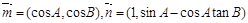 ,求
,求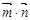 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com